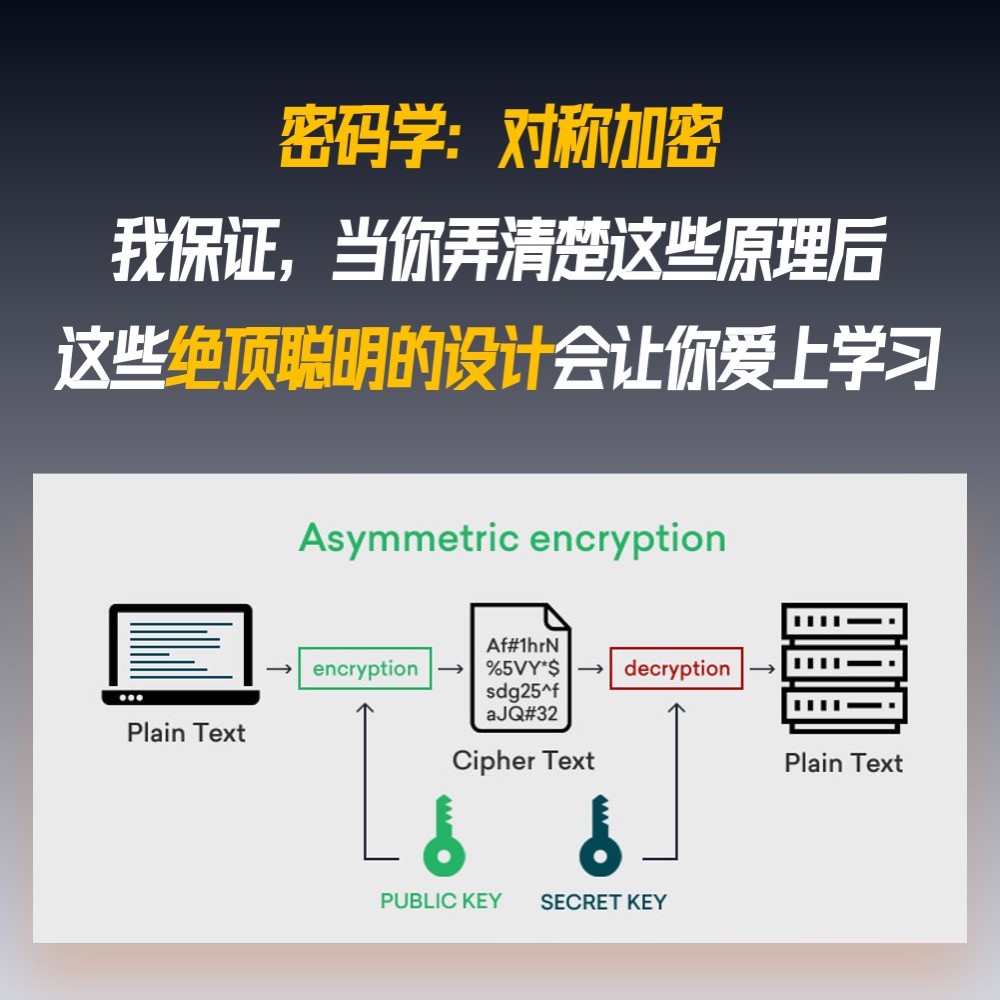
分组密码
将被加密明文划分成一个一个的分组,输入n比特明文分组,输出n比特密文分组。
若映射可逆,具有 x^n! 种替换可能性。
如以下示例,每个4比特输入唯一映射为另一个4比特输出。
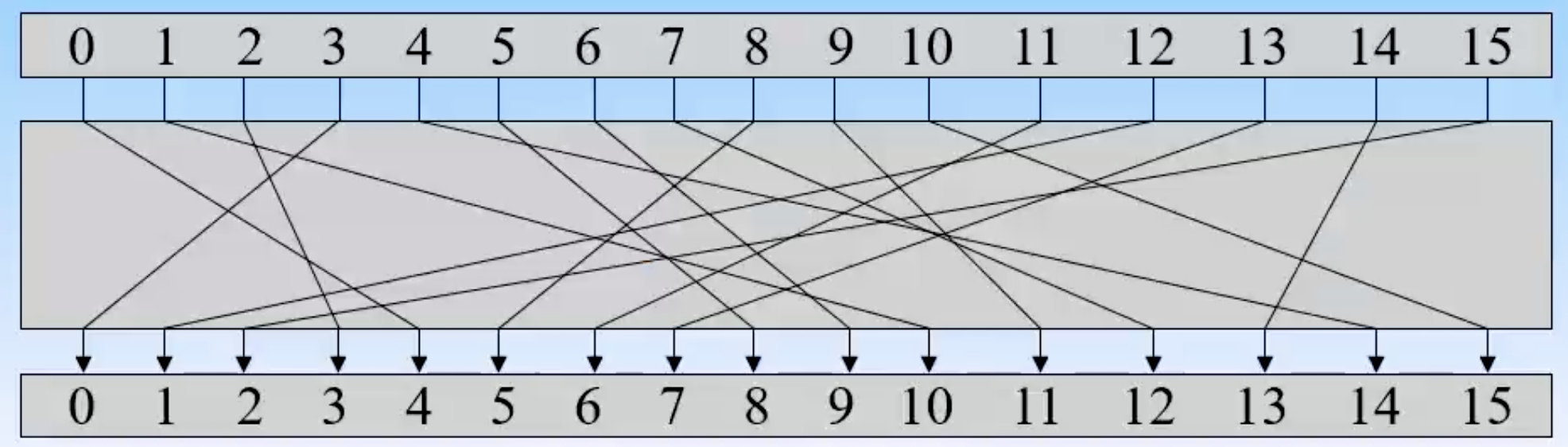
Feistel密码结构
什么是Feistel密码结构
1973年由IBM的Horst Feistel首次提出,通过将明文分组分成左右两半部分
- 左半部分:采用替换操作,
- 右半部分:采用基于子密钥的轮函数(包括替换和置换组合操作)进行混淆,
如此经过n轮迭代处理后再重新合并组成密文分组
Feistel密码结构流程图
将Feistel公式化,首先来看加密过程,
- 每一轮的左半部分是上一轮的右半部分
- 每一轮的右半部分是 (上一轮的右半部分进入一个F操作,且要输入这一轮的密钥K_i ),然后产生的解再与上一轮的左半部分进行异或操作
那清楚了加密的过程,能不能反推解密的公式呢?答案是可以的,由于RE_ {i-1}等于LE_i,所以解密公式的各个变量都是已知的。所以分组密码是可逆的。

用流程图画出来就是这样的:
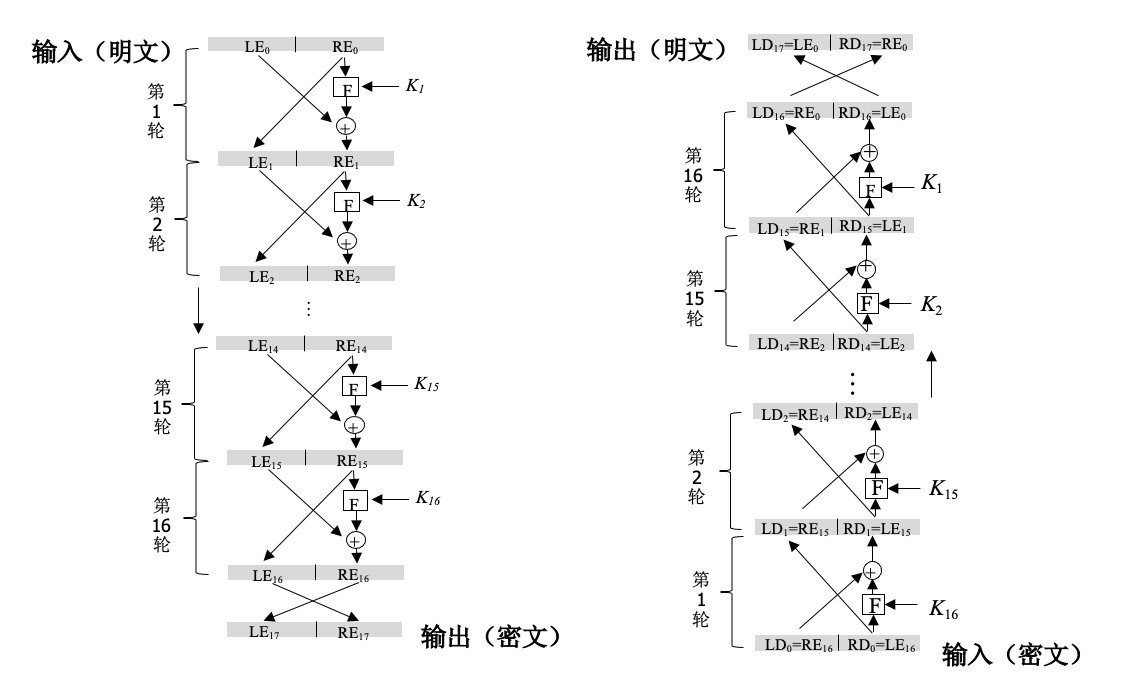
那F操作(F函数)是不是可逆的吗?但其实F操作没有要求,可逆也可以 ,不可逆也可以。因为加密的时候用的是F操作,解密的时候也是用的F操作,所以在加密解密的F操作都是正操作,也就都没有用到F操作的逆操作。这里面很大的原因还是Feistel的巧妙结构,分为左右两个部分才能使得F操作可以不可逆,如果只有一个部分那就要求F操作必须可逆。右半部分其实是已知继承下来的,可以保留上一轮的特性。
### Feistel密码设计要素
- 分组大小:越大的分组越安全,但减小了加密/解密速率
- 密钥大小 :越长的密钥越安全
- 迭代轮数:越多轮越安全。经典是16轮
- 子密钥生成算法:越复杂越难破解
- 论函数:越复杂越难破解
- 快速软件加密/解密:嵌入式实现,要求快速执行速度
- 容易分析:如果算法能被简明清楚地解释,则容易分析该算法的弱点并因此给出对其强度更高级别的保障。例如,DES 不具有容易分析的性质
数据加密标准(DES)
什么是数据加密标准(DES)
DES是最广泛使用的对称加密方案,由原美国国家标准局 (现在是美国国家标准与技术研究所)于1977年采用。
明文分组长度为 64-bit ,密钥有效长度为56-bit,在基于Feistel网络的基础上,采用16轮迭代,从原始56-bit密钥产生16组子密钥,每一轮迭代使用一个子密钥。
DES介绍
DES 涉及以下操作:
- 初始置换(通过置换矩阵,输入64bit,输出64bit)
- 轮函数操作(F操作)
- 先将输入的64bit分为左右两半部分,每个部分32bit,下面只对右半部分进行操作
- 扩展运算E (输入32bit,输出48bit)
- 与子密钥进行异或操作(输入48bit,子密钥也是48bit,输出48bit)
- 压缩运算 S(输入48bit,输出32bit)(唯一不可逆的操作)
- 置换运算P (输入32bit,输出32bit)
- 与上一轮的左半部分进行异或运算(输入32bit,输出32bit),得到这一轮的右半部分
- 这一轮的左半部分等于上一轮的左半部分(32bit)。这一轮的右半部分(32bit)通过上面的操作已经得到了。
- 子密钥产生算法
- 置换选择1(输入64bit,输出56比特)
- 将56bit分为2个28bit的部分(输入56bit,输出2*28bit)
- 对2个28bit的部分进行循环左移操作(输入2*28bit,输出 2 * 28bit)
- 将2个28bit部分合并成一个56bit(输入2*28bit,输出56bit)
- 置换选择2(输入56bit,输出48bit),得到这一轮的子密钥
- (利用这个子密钥跟轮函数扩展运算后的的48bit进行异或操作)
- 逆初始操作(通过逆置换矩阵,输入64bit,输出64bit)

接下来介绍每一个操作的具体实现
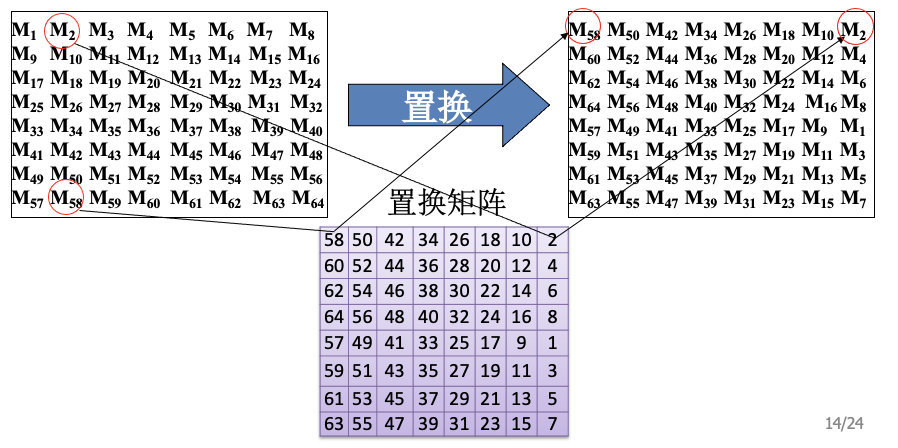
初始置换
DES会有标准的置换矩阵,在实现算法的时候不要改动这些标准的矩阵,虽然改动了也可以完成加解密,但是与其他人通信的时候别人使用标准的置换矩阵就解密不出来了。
初始置换其实是一个矩阵置换(不是映射,这里只是改变了位置)的过程,这里左边是64比特明文输入,下边是标准的置换矩阵,我们需要对明文通过置换矩阵进行初始置换得到右边的矩阵(这里先称为密文矩阵,但其实不是最终的密文矩阵,只是第一步加密得到的)。
比如,置换矩阵的第一行第一列是58,我们在明文矩阵中找到第58个比特,然后放到密文矩阵的第一行第一列;置换矩阵的第一行第二列是50,所以在明文矩阵中找到第50个比特,然后放到密文矩阵的第一行第二列。按照这种方式,一一置换,得到第一次置换的矩阵。
轮函数
轮函数也就是前面Feistel网络的F操作(round function)。将输入的64比特分为左右两半部分,每个部分32比特。
对右半部分数据 R_{i-1} 进行如下操作:
- $R_{i-1}$通过选择扩展运算$E$ 扩展成48-bit数据
- 与子密钥K_i异或生成新的48-bit数据
- 经过压缩运算 S 变成32-bit数据
- 进行置换运算P (可逆的,跟之前的置换操作原理是一致的)
- 与左半部分数据L_{i-1}进行异或
这一步完成之后,得到的就是下一轮的右半部分,而下一轮的左半部分就从上一轮的右半部分直接继承下来。如此循环。

扩展运算
我们说整个加密过程会先分组为64比特明文的输入,每个64比特再分为左右两部分,每个部分32比特,在论函数的第一步是对32比特进行扩展运行E,将32比特通过扩展矩阵变为48比特。
具体过程如下图所示,其实就是添加冗余。可以看到生成的扩展矩阵(48比特)第2列到第5列的值是原封不动加入进来的,第1列和第6列再从原来的32比特矩阵对应取出。(跟前面讲过的初始置换矩阵原理是一致的)
这里需要思考从48比特置换回32比特的操作(多到1)是可逆的吗?其实是可逆的,只需要将冗余去掉就得到原来的矩阵了。

压缩运算
DES中压缩运算S则是非线性的(意思就是不可逆的),而其它运算都是线性的(可逆的)。 压缩运算S不易于分析,提供了更好的安全性。
压缩的总体操作:是将扩展运算后产生的48比特,与子密钥异或操作后还是48比特,再将这48比特分为8个6比特的小组,再通过映射规则(跟之前的置换运算不一样,映射操作是不可逆的)将每个6比特压缩成4比特,这样就变成整体 8*4比特 = 32比特了。

那具体的映射规则是怎么样呢?
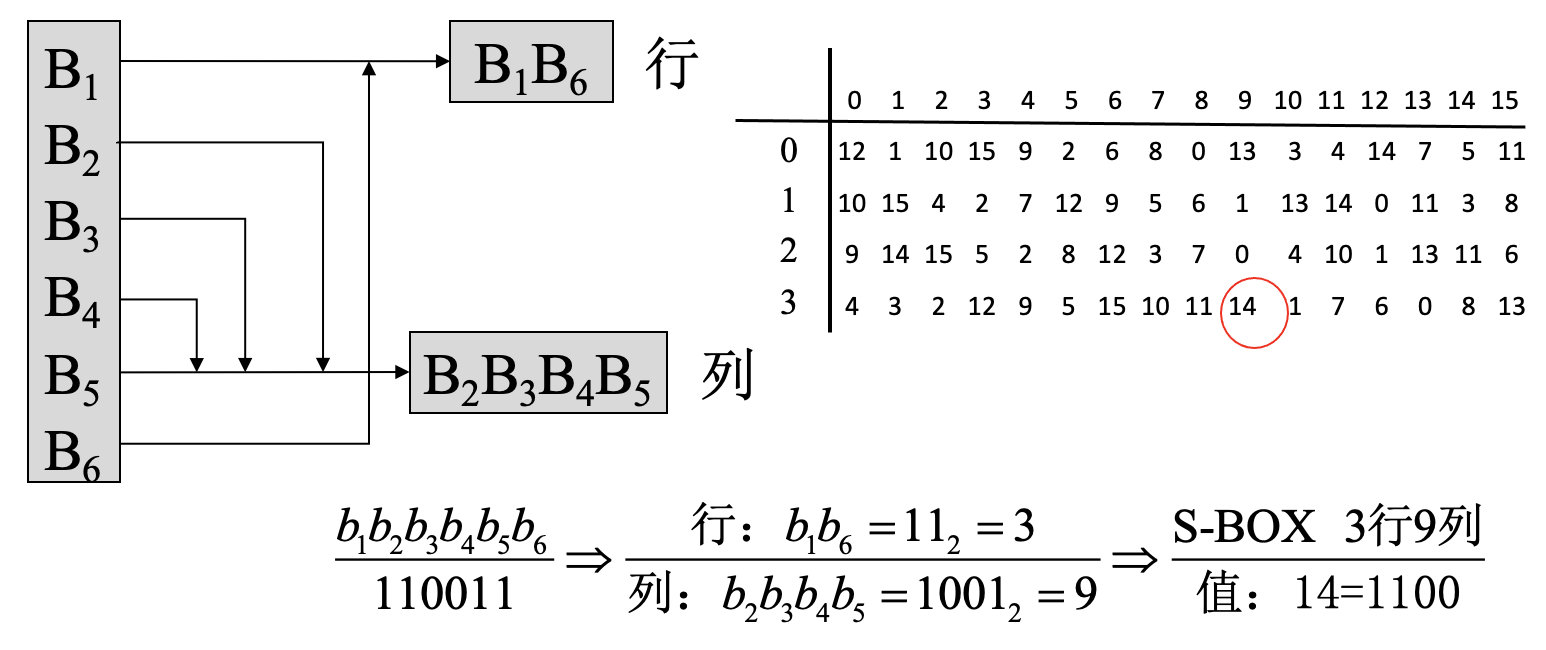
前面说的分成8个6比特的小组,我们称为S_1…S_8$一共8个S-BOX,每个S-BOX之下都有一张标准化的表(做算法的时候不要改动这些表,表中最大的值是15,因为最后要转化为4比特),且每个S-BOX的表都是不一样的。这里的规则是这样的:
- 输入的是6比特:b_1b_2b_3b_4b_5b_6,比如这里输入110011
- 将b_1b_6提取出来当作行,将b_2b_3b_4b_5提取出来当作列,那么提取出来的行是11(转为十进制是3),列是1001(十进制是9)
- 根据十进制的行是3,列是9,在S-BOX中找到第3行第9列的数字是14
- 再将14转化为二进制,是1100,这个1110就是压缩后的4比特。
如此,将全部8个6比特的小组都转化4比特。这里因为S-BOX表中有重复的值,所以逆操作是不唯一的,所以是压缩操作是不可逆的运算。
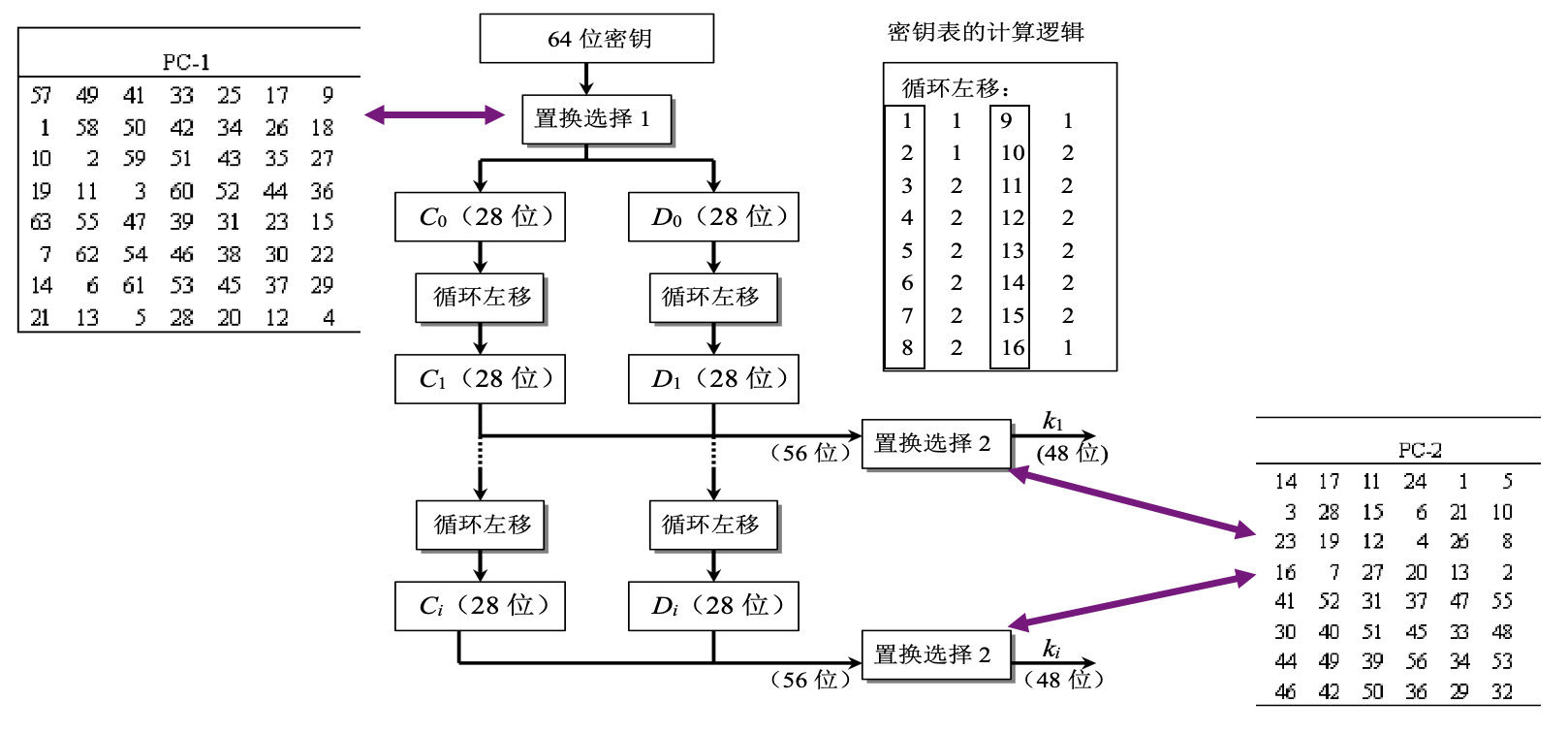
子密钥生成算法
输入的是64比特的密钥,通过置换选择1(PC-1是87=56比特)变成56比特,再将56比特分为228比特,分为是C和D两部分,每部分再根据密钥表的计算逻辑循环左移,再将左移后的两部分C和D合并成56比特做一次置换运算2(PC-2是8 * 6= 48比特),变成48比特,这就是每一轮的子密钥,用这个子密钥去跟轮函数中扩展运行后的48比特寄存器做异或运算。
循环左移的逻辑这里解释一下,以4比特的0010为例,根据密钥表的计算逻辑,第一轮左移1位,第二轮左移1位,第三轮左移2位,分别变成0010 -> 0100 -> 1000 -> 0010,如此循环,移动16轮,移动一轮置换一轮,生成这一轮的子密钥。
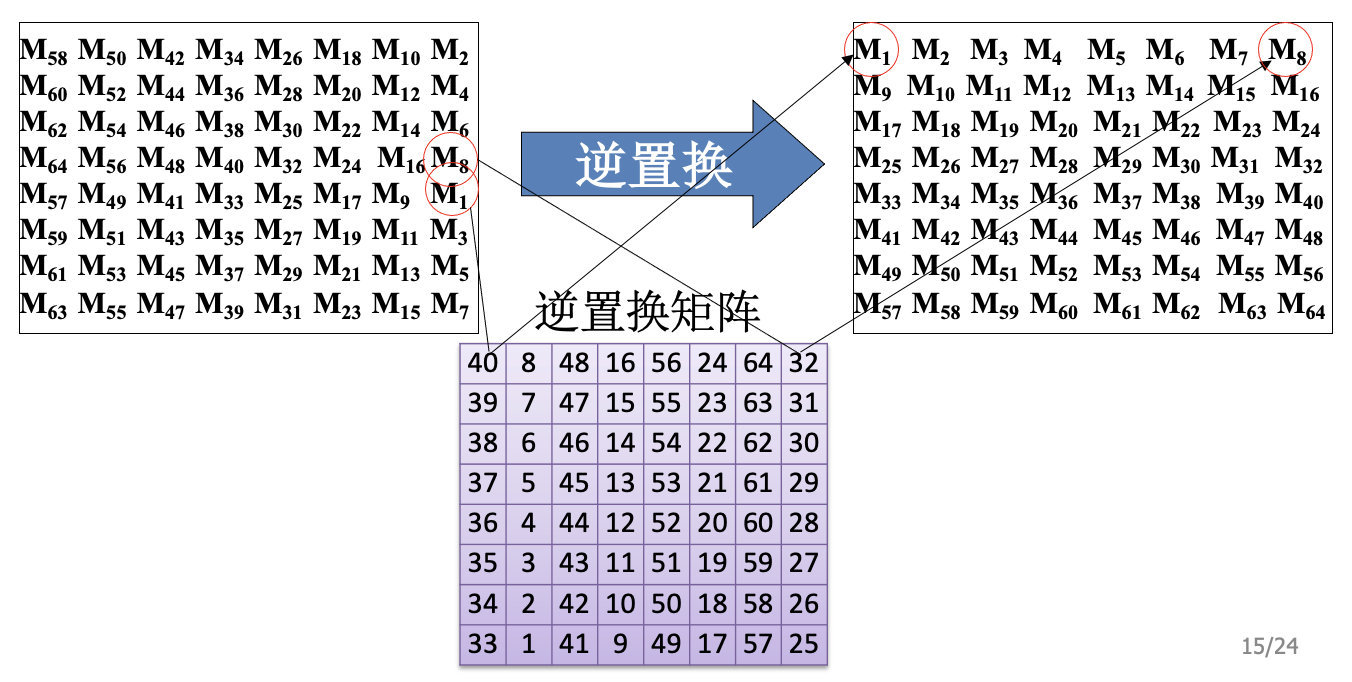
逆初始置换
逆初始置换的概念其实跟前面讲过的初始置换是有联系的,我们前面通过置换矩阵将M1…M64的明文矩阵打乱为密文矩阵,这里的逆初始置换操作跟初始置换是一样的,只是使用的是的逆置换矩阵。