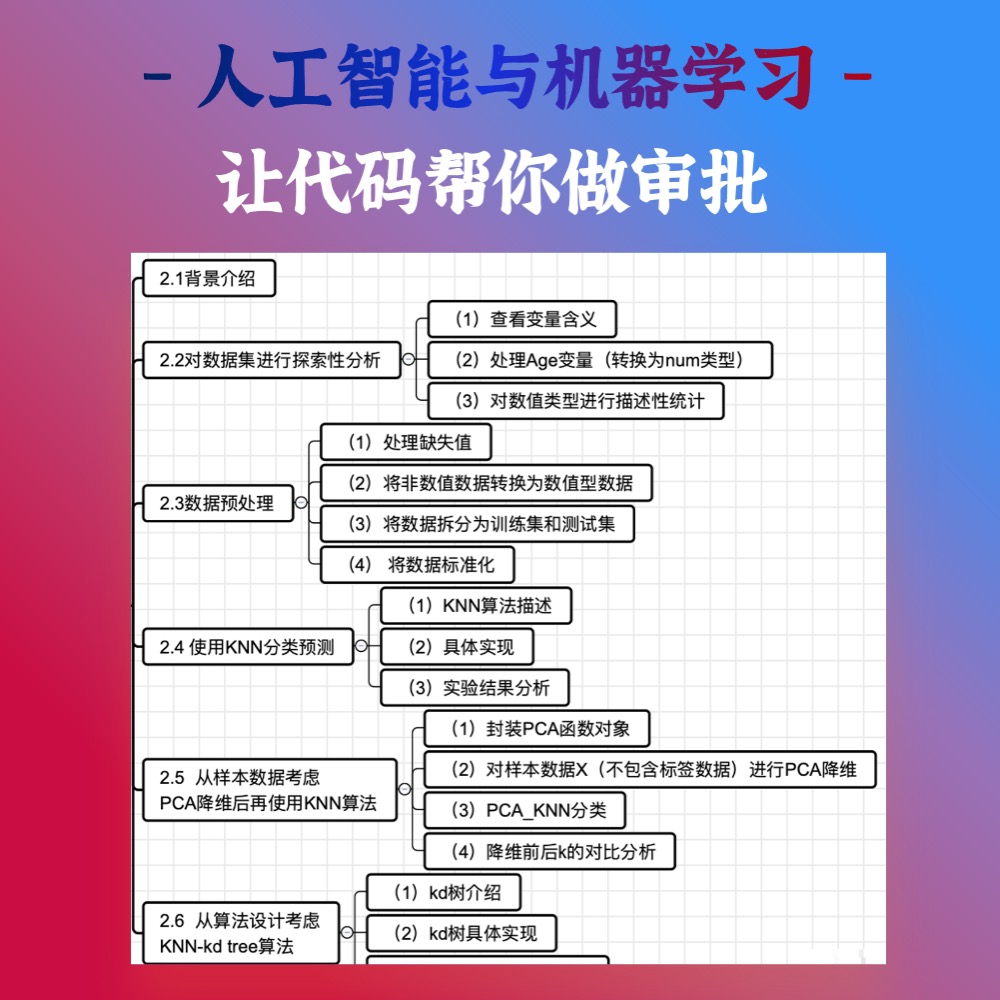
本次实验围绕求解八数码问题展开，将问题通过状态空间法进行知识表示，并对比分析了深度优先算法、广度优先算法和基于不同启发式函数的A*搜索算法的实现方案。思维导图如下：

Oops! You forgot to select a pdf file.

完整代码如下：

import time
Statu_saving= {}#用来表名当前状态和前一个状态，便于回溯
MoveString = {}#存储每个可能发生的动作
Movement_Output =[]#输出动作的结果
Statu_distance={}#记录当前状态到目标状态的距离
Fn= {}#总代价函数

class MoveStruct: #定义状态结构 xxf
    def __init__(self):
        self.NextLoc = [];
        self.Movement ={};

Moveable=MoveStruct()
Moveable.NextLoc=[[1,3],[0, 2, 4],[1, 5],[0,4,6],[1,3,5,7],[2,4,8],[3,7],[4,6,8],[5,7]]
Movement={0:[0,"Left",0,"Up"], 1:["Right",0, "Left",0,"Up"],2:[0,"Right",0,0,0, "Up"],
                    3:["Down",0,0,0,"Left",0,"Up"],4:[0,"Down",0,"Right",0,"Left",0,"Up"],5:[0,0,"Down",0,"Right",0,0,0,"Up"],
                  6:[0,0,0,"Down",0,0,0,"Left"],  7:[0,0,0,0,"Down",0,"Right",0,"Left"],8:[0,0,0,0,0,"Down",0,"Right"]}

def swap_chr(a, i, j):#无信息搜索算法：用于移动位置的交换函数 xxf
    if i > j:
        i, j = j, i
    b = a[:i] + a[j] + a[i+1:j] + a[i] + a[j+1:]#切片方法，返回交换后的状态
    return b

def swap_chr_A(a, i, j, distance, destLayout):#A*（Distance）xxf
    if i > j:
        i, j = j, i
    b = a[:i] + a[j] + a[i+1:j] + a[i] + a[j+1:]
    fn = distance+Distance_Compute(b, destLayout) #fn,储存代价值
    return b, fn

def swap_chr_a(a, i, j, distance, destLayout):#A*（Number）xxf
    if i > j:
        i, j = j, i
    b = a[:i] + a[j] + a[i+1:j] + a[i] + a[j+1:]
    fn = distance+Number_Compute(b, destLayout) #fn,储存代价值
    return b, fn

def Distance_Compute(srcLayout,destLayout):#基于曼哈顿距离计算代价，返回代价值 xxf
    sum=0
    a= srcLayout.index("0")#排除空格的下标位置，防止干扰
    for i in range(0,9):#循环其他每个位置
        if i!=a:
            sum=sum+abs(i-destLayout.index(srcLayout[i]))#计算当前状态和目标状态的代价
    return sum

def Number_Compute(srcLayout,destLayout):#返回错码和正确码错位个数之和 xxf
    sum=0
    a= srcLayout.index("0")
    for i in range(0,9):
        if i!=a:
            if(srcLayout[i]!=destLayout[i]):#如果发生错位
                 sum+=1#计算当前状态和目标状态的代价
    return sum

def judge(srcLayout, destLayout):# 判断起始状态是否能够到达目标状态 xxf
    src = 0
    dest= 0
    for i in range(1, 9):
        fist = 0
        for j in range(0, i):
            if srcLayout[j] > srcLayout[i] and srcLayout[i] != '0':
                fist = fist + 1
        src = src + fist
    for i in range(1, 9):
        fist = 0
        for j in range(0, i):
            if destLayout[j] > destLayout[i] and destLayout[i] != '0':
                fist = fist + 1
        dest = dest + fist
    if (src % 2) != (dest % 2):  # 同奇同偶时才可达的
        return -1, None
    else:return 0

def solvePuzzle_DFS(srcLayout, destLayout):#深度优先搜索算法 xxf
    Statu_saving[srcLayout] = -1 #初始化字典
    Answer_Solving = []
    Answer_Solving.append(srcLayout)#当前状态存入列表

    while len(Answer_Solving) > 0: #如果栈中存在状态
        curLayout = Answer_Solving.pop()#出栈
        if curLayout == destLayout:#判断当前状态是否为目标状态
            break#如果是目标状态，则出栈

        ind_slide = curLayout.index("0")#获得空格位置的下标,
        lst_shifts = Moveable.NextLoc[ind_slide]#当前可进行交换的位置集合
        for nShift in lst_shifts:
            newLayout = swap_chr(curLayout, nShift, ind_slide)#进行交换
            if Statu_saving.get(newLayout) == None:#判断交换后的状态是否没有查询过
                Statu_saving[newLayout] = curLayout#如果状态没有查询过，则将其存到字典里面，
                Answer_Solving.append(newLayout)#存入集合
                MoveString[newLayout]=Movement[ind_slide][nShift]#每一个动作存在对应的MoveString中
                if newLayout == destLayout:  # 判断当前状态是否为目标状态
                    break  # 如果是目标状态，则出栈

def solvePuzzle_BFS(srcLayout, destLayout):#广度优先搜索算法BFS xxf
    Statu_saving[srcLayout] = -1
    Answer_Solving = []
    Answer_Solving.append(srcLayout)

    while len(Answer_Solving) > 0:
        curLayout = Answer_Solving.pop(0) #跟DFS一样，只需将此处修改为队列实现
        if curLayout == destLayout:
            break

        ind_slide = curLayout.index("0")
        lst_shifts = Moveable.NextLoc[ind_slide]
        for nShift in lst_shifts:
            newLayout = swap_chr(curLayout, nShift, ind_slide)
            if Statu_saving.get(newLayout) == None:
                Statu_saving[newLayout] = curLayout
                Answer_Solving.append(newLayout)
                MoveString[newLayout]=Movement[ind_slide][nShift]
                if newLayout == destLayout:
                    break


def solvePuzzle_A(srcLayout, destLayout):#A*（Distance+Number） xxf
    Statu_saving[srcLayout] = -1 #初始化字典
    Statu_distance[srcLayout]= 1
    Fn[srcLayout] = 1 + Distance_Compute(srcLayout, destLayout) #Distance的A*算法，计算总代价：实际要走的代价+预测的代价
    #Fn[srcLayout] = 1 + Number_Compute(srcLayout, destLayout) #Number 的A*算法
    Answer_Solving = []
    Answer_Solving.append(srcLayout)#当前状态存入列表，跟无信息搜索一致
    while len(Answer_Solving) > 0:#当存在可移动的状态
        curLayout = min(Fn, key=Fn.get)#比较字典中value，返回Key，找到最小代价作为下一个起点
        del Fn[curLayout]#找到最小代价后删除curLayout中的变量
        Answer_Solving.remove(curLayout)#找到最小fn后还要移除“curlayout”这个对象
        if curLayout == destLayout:#判断当前状态是否为目标状态
            break
        ind_slide = curLayout.index("0")# 寻找0的位置。
        lst_shifts = Moveable.NextLoc[ind_slide]#当前可进行交换的位置集合
        for nShift in lst_shifts:#在可以交换的集合中
            #hn是目前的总代价（实际+预测）
            newLayout, hn = swap_chr_A(curLayout, nShift, ind_slide, Statu_distance[curLayout] + 1, destLayout)#Distance的A*算法
            #newLayout, hn = swap_chr_a(curLayout, nShift, ind_slide, Statu_distance[curLayout] + 1, destLayout)#Number的A*算法
            if Statu_saving.get(newLayout) == None:#判断交换后的状态是否已经查询过
                Statu_distance[newLayout] = Statu_distance[curLayout] + 1 #存入走的路程，走了1步
                Fn[newLayout] = hn#存入fn,当前状态对应的代价
                Statu_saving[newLayout] = curLayout#定义前驱结点
                Answer_Solving.append(newLayout)#存入集合
                MoveString[newLayout] = Movement[ind_slide][nShift]  # 动作存在对应的MoveString
                if newLayout == destLayout:  # 判断当前状态是否为目标状态
                    break  # 如果是目标状态，则出栈

def solvePuzzle(srcLayout, destLayout): #xxf
    Answer_Output = []#当全部状态完成
    Answer_Output.append(destLayout)
    curLayout=destLayout
    while Statu_saving[curLayout] != -1:#当等于-1时，意味着可以退出循环，因为第一个初始状态的字典value是-1
        curLayout = Statu_saving[curLayout]#按照最后状态往前逆推回溯
        Answer_Output.append(curLayout)#将每一个状态保存
    Answer_Output.reverse()#用reverse得到顺序输出
    for answer in Answer_Output:
        if(answer!=srcLayout):
            Movement_Output.append(MoveString[answer])
    return 0, Answer_Output#如同奇同偶，则可达

if __name__ == "__main__": #xxf
    start =time.time()
    srcLayout  ="012345678" #输入初始状态
    destLayout ="123045678" #输入目标状态
    if(judge(srcLayout,destLayout)==0):
        #solvePuzzle_DFS(srcLayout, destLayout)  #DFS
        #solvePuzzle_BFS(srcLayout, destLayout)   #BFS
        solvePuzzle_A(srcLayout, destLayout)    #A*
        retCode, lst_steps= solvePuzzle(srcLayout, destLayout)
        for number in range(len(lst_steps)):
            if(lst_steps[number]!=srcLayout):
                print("The " + str(number) + "th move is：")
                print(lst_steps[number][:3])  # 切片，为了显示美观
                print(lst_steps[number][3:6])
                print(lst_steps[number][6:])
                print("-------------")
        end = time.time()
        print("The move action is: ", Movement_Output)
        print("The number of moves is: ", len(Movement_Output))
        print("The time consumed is：" + str(end - start) + " s")  # 查看运行时间（秒）
    else:
        print("Cannot be achieved")#逆序性不满足