本项目实现金融数据的降维,笔者基于个人对普惠金融的研究兴趣,在初步进行文献调研后,决定使用PCA算法对我国普惠金融发展水平进行综合评价分析,在这个过程中,对PCA算法进行了较为深入的理解和扩展,最后对各省的普惠金融发展水平进行了排名,并画出了我国普惠金融发展水平地图。这是一个将所学算法知识应用于研究兴趣的过程,收获颇丰,也对机器学习这门课程产生了更加浓厚的兴趣。同时,笔者也感叹数据获取来之不易,即使有很好的算法,如果没有质量好的数据,也是巧妇难为无米之炊…
背景介绍
普惠金融是指金融机构根据机会平等和商业可持续性发展原则,向所有需要的个人和企业,按照合理的定价提供方便、快捷和可靠的全方位、多层次金融服务[1]。当前,中国普惠金融整体发展水平还有待提高,尤其是区域间(不同省际之间、东中西部之间)发展不平衡,差异大。因此,构建合理、协调、有效的普惠金融发展水平综合评价指标体系,采用恰当的综合评价方法进行可靠的综合评价,对准确分析不同区域间的差异,厘清制约各地区普惠金融发展的主要因素,已成为中国金融改革与发展的重要理论及现实问题,也是当前金融学界的研究热点和难点问题。
而根据文献调研,在综合评价中,主成分分析可以排除评价过程的人为干扰,提取原有指标的绝大部分信息形成主成分及权重,保持评价结果的客观性[2],按照影响我国普惠金融发展水平多个强相关性的实测变量通过数学降维的方法,形成具有代表性的要素变量。
基于对普惠金融的研究兴趣,笔者将在综述有关文献的基础上,建立适合中国普惠金融发展水平综合评价的指标体系,运用本课程所学的PCA方法对省际普惠金融发展水平进行综合评价和排序分析。
数据说明
在普惠金融发展水平的评价上不能用投入、产出单一的价值指标去衡量,而需要考虑到各个方面,结合《2019年中国普惠金融发展报告》公布的信息和依据相关文献可以得出[3],普惠金融发展水平的主要影响因素有GDP(亿元)、银行业金融机构网点数(个)、银行业金融机构从业人员数(人)、资产总额(亿元)、本外币存款余额(亿元)、本外币贷款余额(亿元)、保费收入(亿元)、保险密度(元/人)、保险深度(%)等。
笔者将以2019年基于上述指标的普惠金融发展水平进行分析,所有的评价指标数据均来自公开资料,包括《中国统计年鉴》《中国保险年鉴》《中国金融年鉴》和《中国各省市金融运行报告》,由于都是公开资料数据,考虑到可比性、公开性和可获得性,没有对数据做人为修改和调整。原始数据如图2所示:
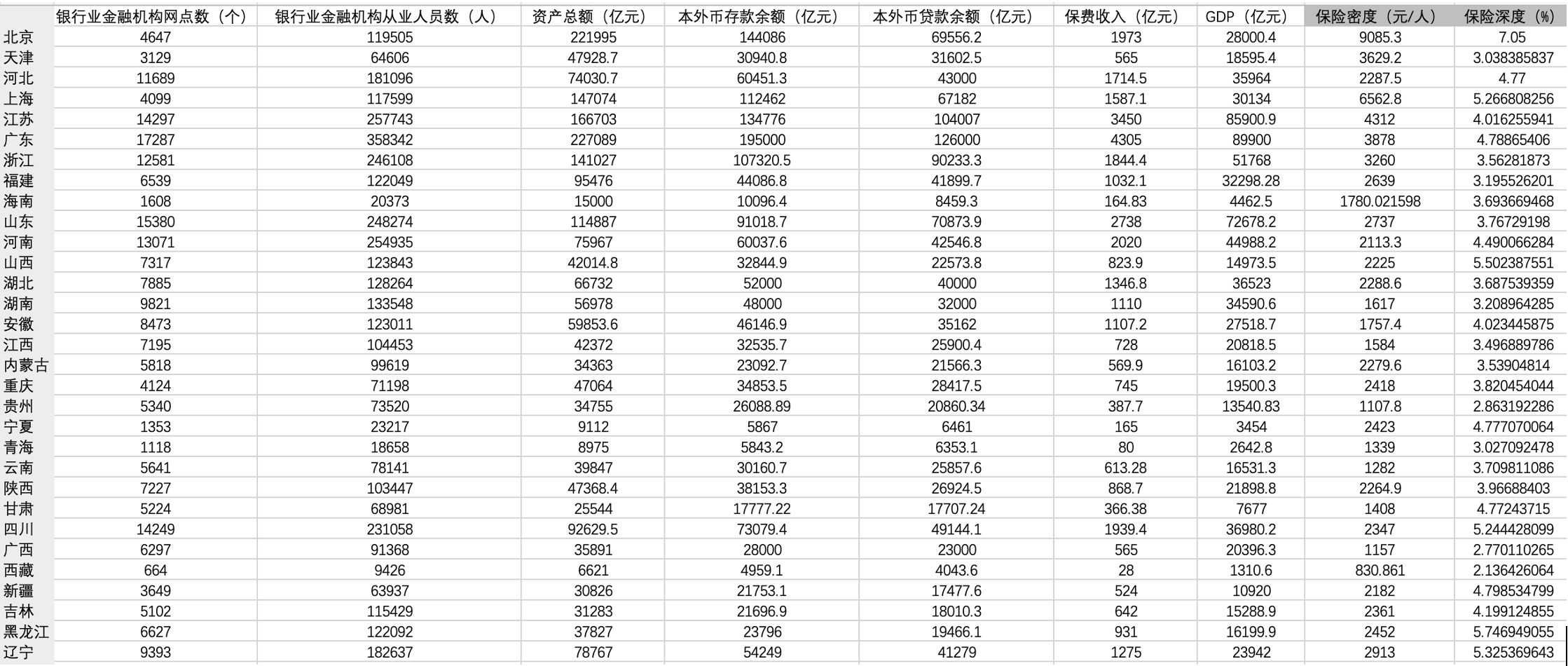
图2: 普惠金融发展水平评价指标原始数据
PCA算法原理
PCA算法描述如图3所示:

图3 PCA算法描述[1]
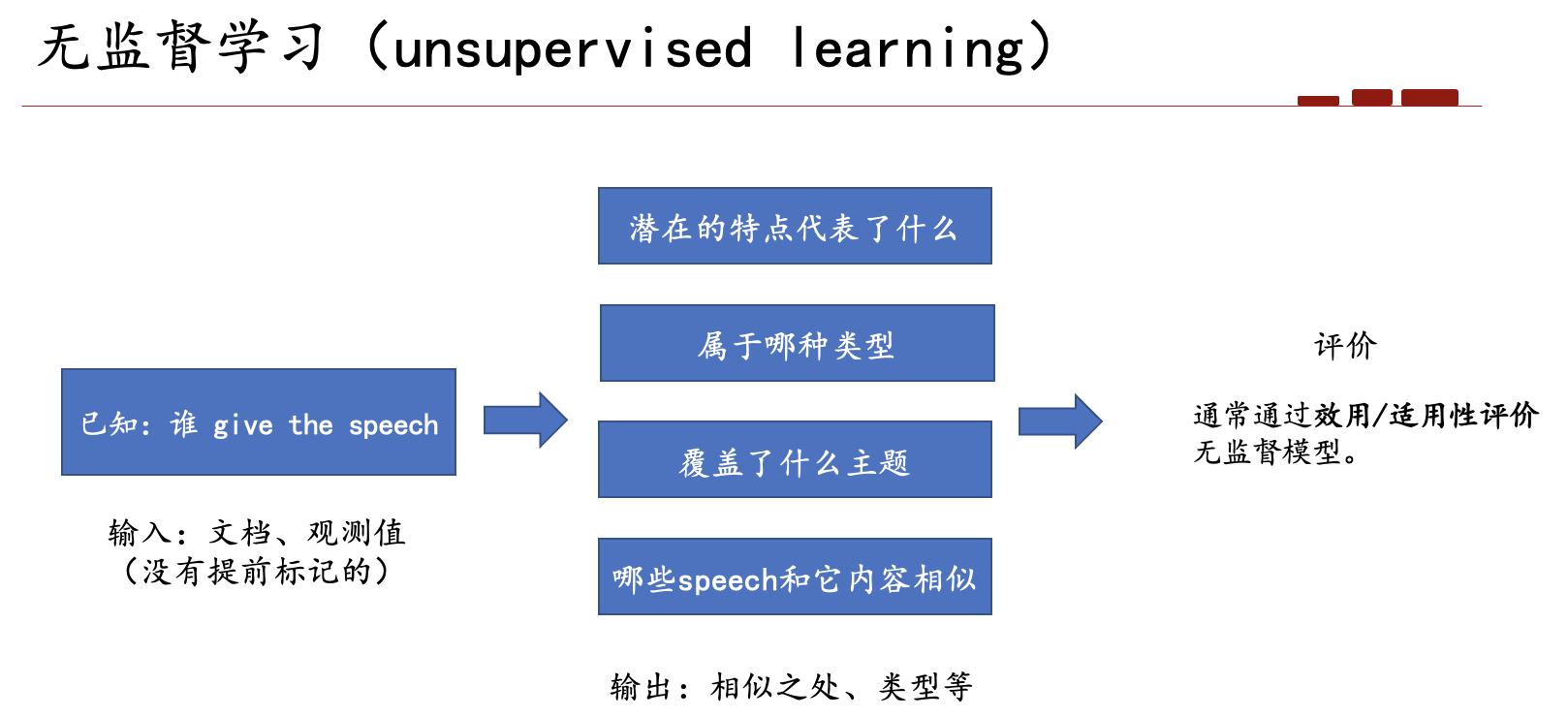
- 无监督学习(unsupervised learning):无标签/无正确答案
监督学习(supervised learning):有标签/有正确答案
- 无标签:有一些重要的潜在的structure
- 我们的目标:用fundamental techniques to access these structure,以及解释所得到的结果。

- 主成分的特点:主成分之间彼此线性无关(正交),是原始变量的线性组合。
- 主成分的解释:取决于成分之间的相互关系和原始变量的相互关系,我们称之为“因子载荷”(主成分系数=因子载荷/特征值的算术平方根)。
- 每个原始observation在每个主成分上都有一个score系数,可以看着是它的“投影”。
- Result:将原始的observations映射到更低维的空间中。
- Method:decomposition of the cov matrix or singular value decomposition(奇异值分解) of data matrix.
- 存在问题:降维后,由于失去了标签,我们可能无法理解每个维度的含义。
分析过程
导入数据
导入头文件
import pandas as pd
import numpy as np
import time
import matplotlib.mlab as mlab
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import xlrd
import seaborn as sns
使用语句df = pd.read_excel(‘PCA_finance2.xlsx‘)将数据集导入,同时,考虑到pandas库中文字体不兼容的问题,笔者将DataFrame的index和columns修改成英文格式
import pandas as pd
df = pd.read_excel('PCA_finance2.xlsx')
df
df = pd.read_excel('PCA_finance2.xlsx')
df.index = ['BeiJing',' TianJin','HeBei','ShangHai','JiangSu','GuangDong','ZheJiang','FuJian','HaiNan','ShanDong','HeNan','ShanXi','HuBei','HuNan','AnHui','JiangXi','NeiMengGu','ChongQing','GuiZhou','NingXia','QingHai','YunNan','ShanXi','GanSu','SiChuan','GuangXi','XiZang','XinJiang','Jilin','HeiLongJiang','LiaoNing']
df.columns = ['Banking','Employees','Assets','Deposit','Loan','GDP','IS_income','IS_density','IS_depth']
df.head()
导入后数据如图5所示:
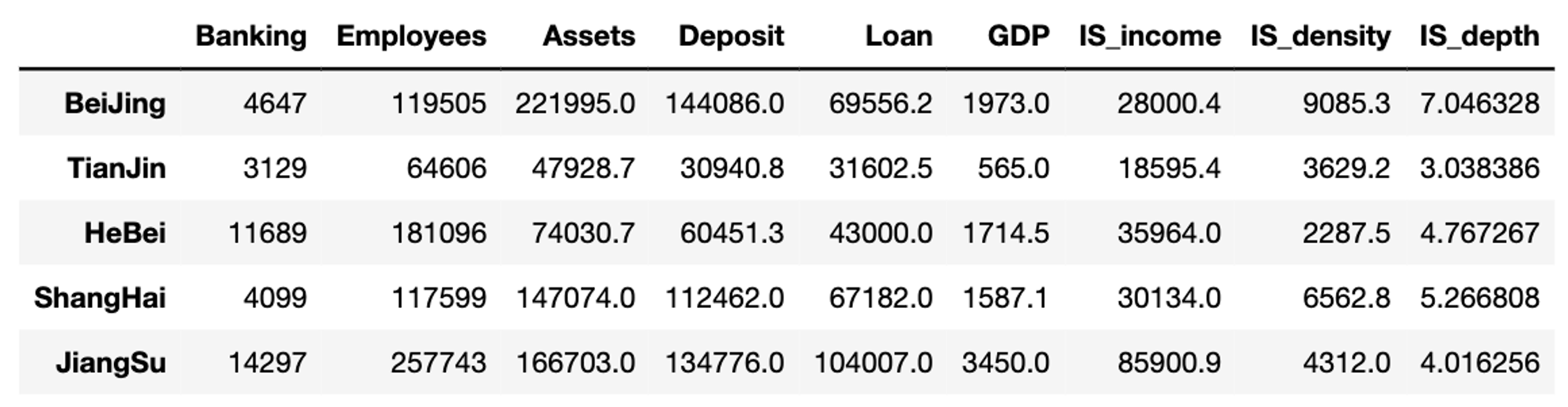
图5 导入后数据
数据初步探索
由于此数据集无缺失值,固无需进行数据预处理,为了进一步理清数据处理步骤,笔者对数据进行进一步探索。
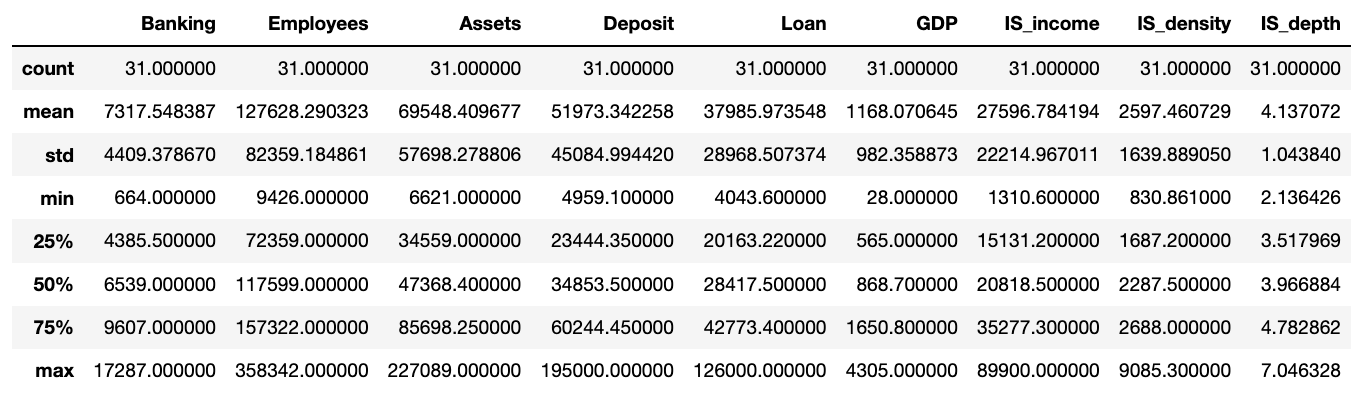
1、使用df.describe()语句可以查看每一个维度上数据的数量,均值,标准差,最小值,最大值及其各分位值的相关信息。
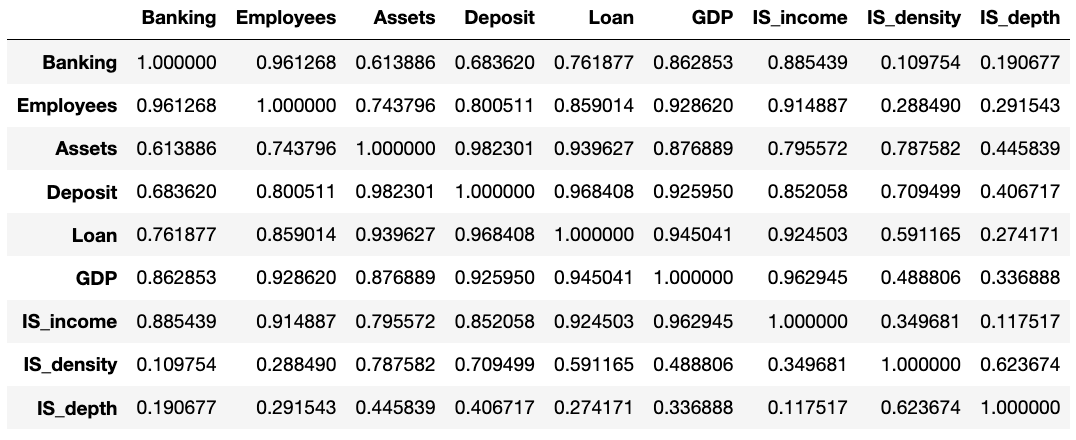
2、使用df.corr()语句可以将每个维度数据的相关性呈现出来,并使用sns.heatmap方法进行热力图可视化,如图6所示,可以发现大部分数据维度都与其他维度呈现出较大的相关性,但是随意删除其中数据又可能会导致信息丢失,所以运用PCA进行降维处理是十分有必要的。
3、使用df.plot.area()方法绘制面积图,面积图使用颜色填充的方式很好地突出了趋势分布信息,例如从图7可以很明显地看到Employees这个维度上数据呈现出比较大地振幅,说明各省之间银行业金融机构从业人员数有着比较明显的差别。

建立PCA模型
Step1: 把df转换numpy矩阵形式,储存在data变量(语句:data = np.mat(df))
Step2: 数据去中心化,即计算每一列数据对应的均值(X_mean = np.mean(data, axis=0)),将每一列的各个数据去中心化 (减去均值)(去中心化的数据储存在dataMax,其中dataMax.shape = (31, 9))
Step3:计算协方差矩阵(covMat = np.cov(dataMax, rowvar=0))(注意:其中一行为一个样本时,covMat=0;当一列为一个样本时,rowvar不为0)
Step4: 计算特征值和特征向量(语句:eigVal, eigVect = np.linalg.eig(np.mat(covMat))
Step5: 调用sklearn库中的minmaxScaler方法来对特征向量做归一化的处理。
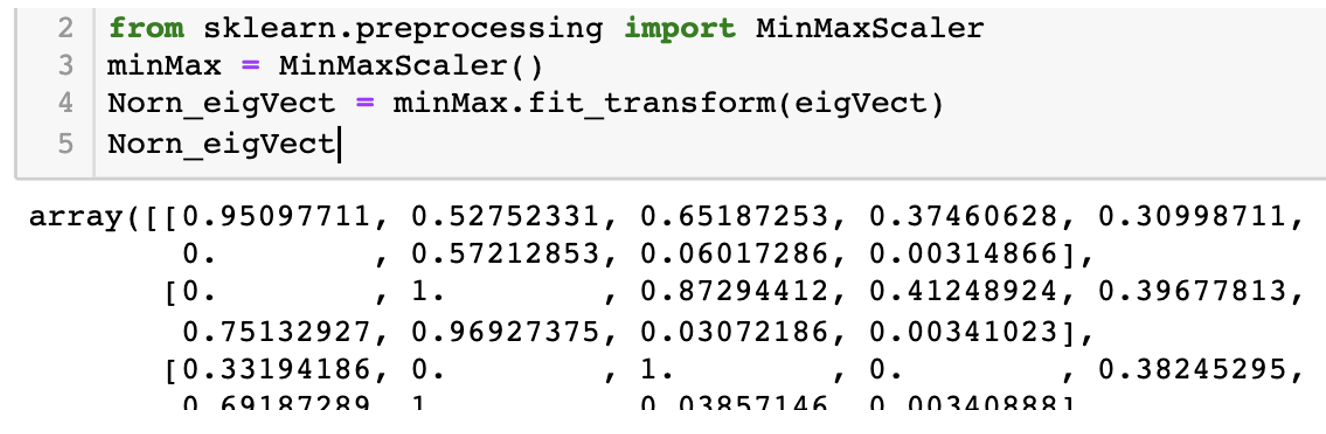
图8:minmaxScaler方法来对特征向量做归一化的处理
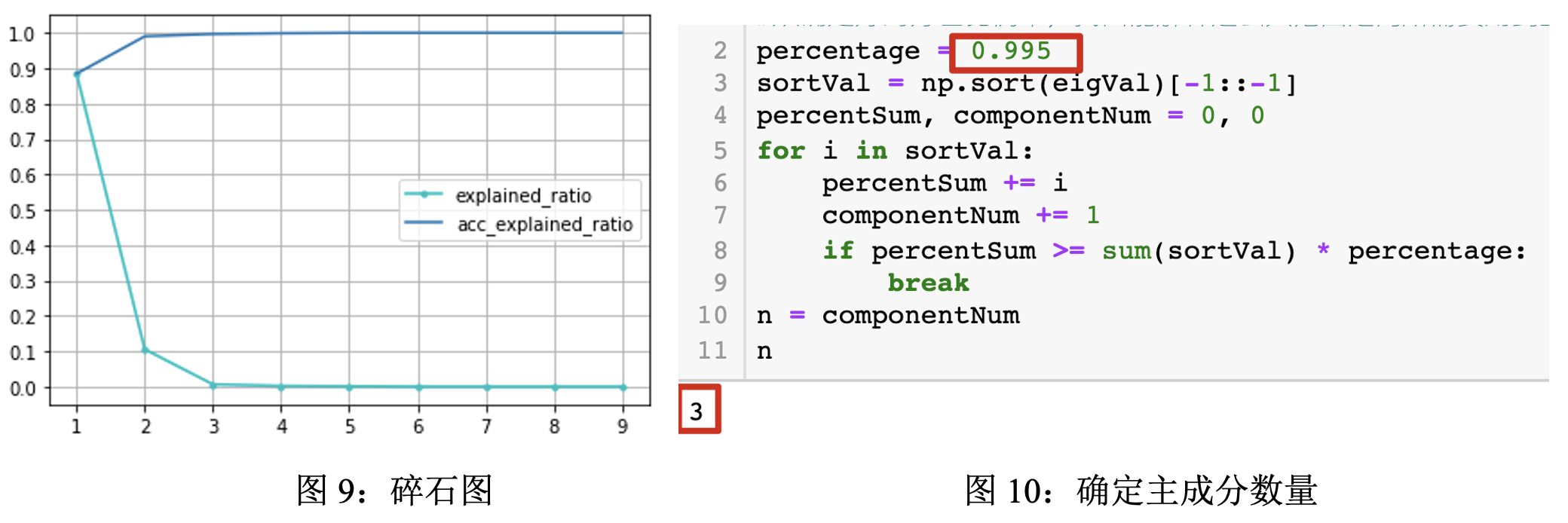
Step6: 根据得到的一系列特征值, 计算各个特征的方差解释率,并画出碎石图。
从表1中,可以直观看到各个特征的方差解释率和累计方差解释率,第1个主成分的解释率为88.46%,第2个主成分的解释率为10.56%,第3个主成分的解释率为0.65%,之后的成分的解释率几乎为0,从图9碎石图也可以看到,直线几乎不再变化。按照常理,本数据使用两个主成分即可解释方差的99%,这里笔者为了可视化图表的展示以及更高的解释率,使用99.5%的方差解释率选取前3个特征作为主成分。
同时为了程序更好的可扩展性,笔者通过np.sort(eigVal)语句对特征值进行排序,使用变量percentage来控制主成分的方差贡献率,可通过要求方差贡献率的大小来确定主成分的个数n。这里笔者要求使用99.5%的方差解释率,可以看到图10输出的n=3。
表1 各个特征的方差解释率
| 特征 | 方差解释率 | 累计方差解释率 |
|---|---|---|
| 特征1 | 88.46% | 88.46% |
| 特征2 | 10.56% | 99.02% |
| 特征3 | 0.65% | 99.67% |
| 特征4 | 0.21% | 99.88% |
| 特征5 | 0.11% | 99.99% |
| 特征6 | 0.01% | 100.00% |
| 特征7 | 0.00% | 100.00% |
| 特征8 | 0.00% | 100.00% |
| 特征9 | 0.00% | 100.00% |
Step7:通过前面确定的主成分个数n = 3,确定主成分的特征向量n_eigVect
笔者通过调研,发现sklearn还有另外一种归一化的方法StandardScale。MinMaxScale是将样本的特征值转换到同一量纲下把数据映射到[0,1]或者[-1, 1]区间内,仅由变量的极值决定,是一种区间放缩法。StandardScale是依照特征矩阵的列处理数据,其通过求z-score的方法,转换为标准正态分布,和整体样本分布相关,每个样本点都能对标准化产生影响。它们的相同点在于都能取消由于量纲不同引起的误差,且都是一种线性变换,都是对向量X按照比例压缩再进行平移。
在对特征向量归一化的过程之中,实际上是使的各个特征的大小范围一致,笔者使用的sklearn中MinMaxScaler的方法,其默认将每种特征的值都归一化到[0,1]之间,归一化后,每个特征均值为0,标准差为1。(归一化后的数值大小范围可根据参数feature_range调整)。所以3个主成分特征向量归一化后的数据如图11所示:
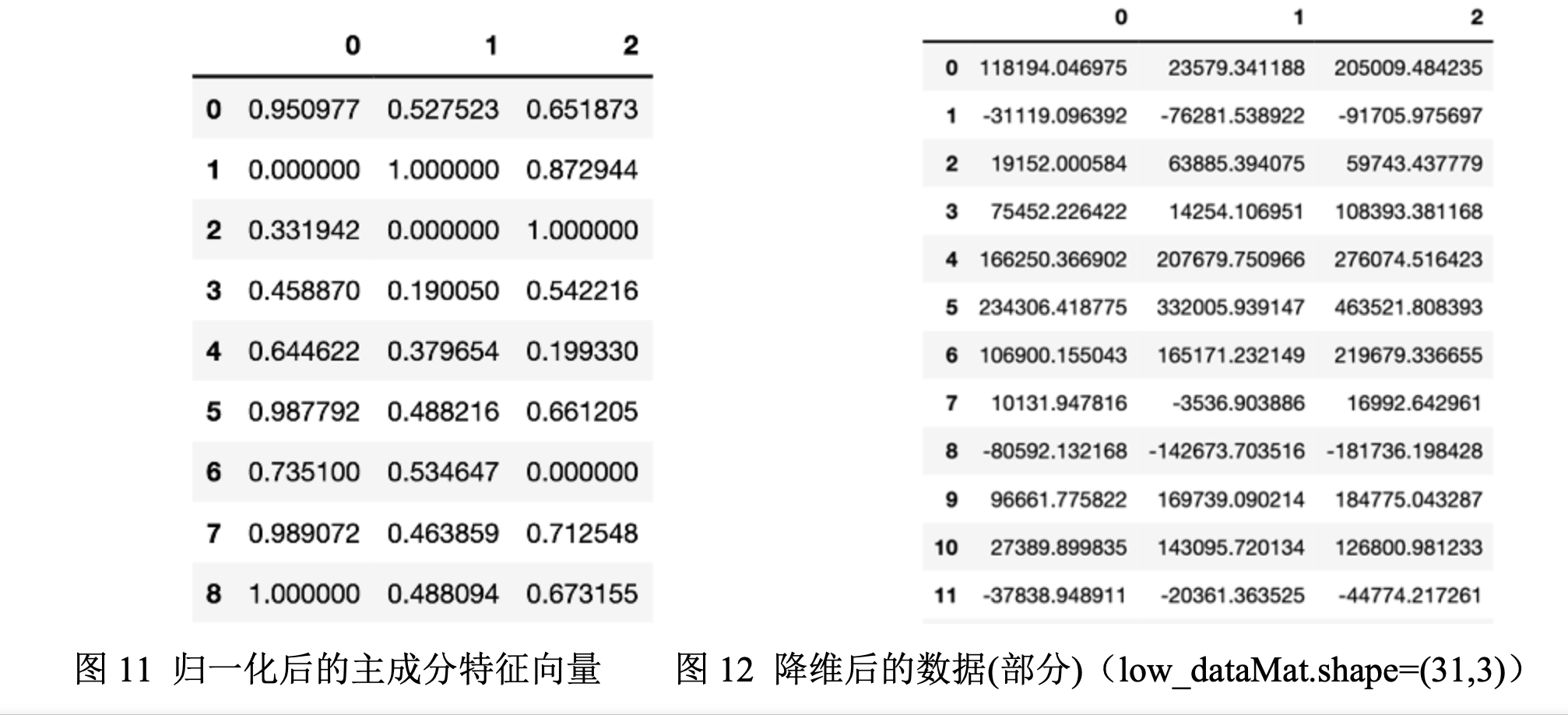
Step8:使用归一化后的主成分特征向量,找到每一个样本在低维空间上的映射(投影),即乘以降维前的数据dataMax(low_dataMat = dataMax * n_eigVect),得到降维之后的31组样本数据low_dataMat。(图12所示)
Step9:对PCA进行可视化,将这31组数据放在以3个主成分为坐标轴形成的散点图中,从图13可以发现这些点虽然是相对分散的,但是对各个样本数据进行普惠金融发展水平评价仍有一定的难度,主要在确定衡量的指标上面。
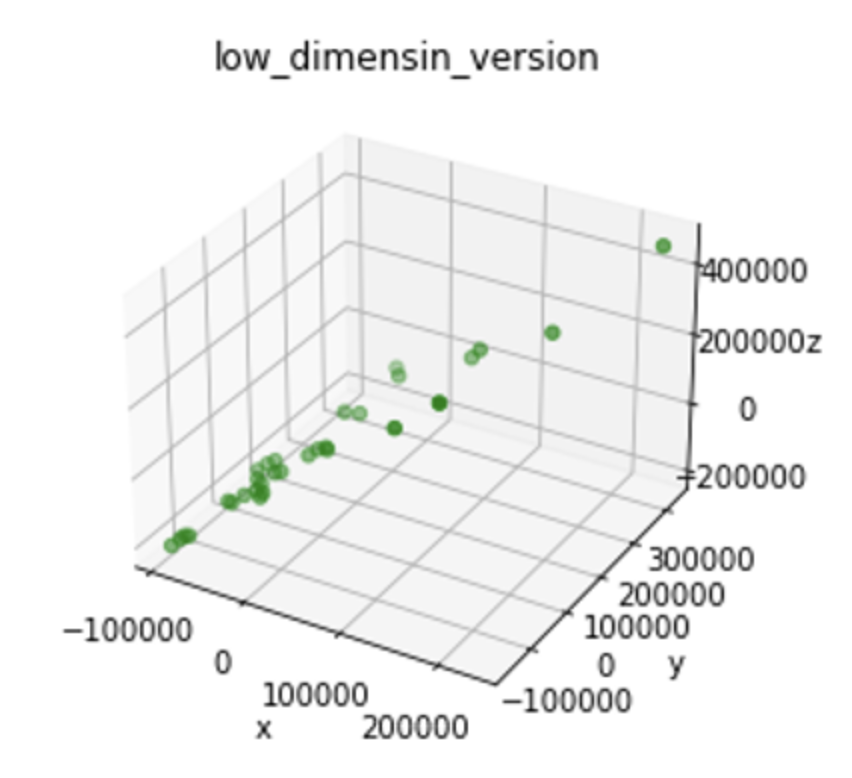
图13 PCA效果可视化
Step10: 为了得到各省的分数,设置一个权重weight(=每一个主成分的方差解释率/总方差解释率),将权重乘以投影后的特征向量作为各省的最终得分,并进行排序(表2所示)和可视化(图14所示)。
#计算权重
weight=[]
for i in range(n):
weight.append(explained_ratio[i] / sum(explained_ratio) )
weight
#存储最终结果
Score=[[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[],[]]
Province=[["北京"],["天津"],["河北"],["上海"],["江苏"],["广东"],["浙江"],["福建"],["海南"],["山东"],["河南"],["山西"],["湖北"],["湖南"],["安徽"],["江西"],["内蒙古"],["重庆"],["贵州"],["宁夏"],["青海"],["云南"],["陕西"],["甘肃"],["四川"],["广西"],["西藏"],["新疆"],["吉林"],["黑龙江"],["辽宁"]]
score=0 #储存每个省份得分总和
dataMaxList=dataMax.tolist()
#计算各省普惠金融发展水平评价得分
for j in range(31):
for z in range(9):
#根据主成分提取的解释程度,计算得分
score+=(dataMaxList[j][z]*n_eigVect[z][0]*weight[0]+dataMaxList[j][z]*n_eigVect[z][1]*weight[1]+dataMaxList[j][z]*n_eigVect[z][2]*weight[2])
Score[j].append(score)
score=0
for i in range(31):
Score[i].append(Province[i])
#排序
Score.sort(reverse=True)
for i in range(31):
print("Rank: ",i+1,Score[i])
表2 我国各省普惠金融发展水平综合评价得分
| 排名 | 省份 | 得分 | 排名 | 省份 | 得分 | 排名 | 省份 | 得分 |
|---|---|---|---|---|---|---|---|---|
| 1 | 广东 | 246158.59 | 12 | 湖北 | 7190.83 | 23 | 内蒙古 | -46605.35 |
| 2 | 江苏 | 171359.10 | 13 | 湖南 | -2256.35 | 24 | 吉林 | -49632.44 |
| 3 | 浙江 | 113812.15 | 14 | 安徽 | -7529.17 | 25 | 贵州 | -52054.47 |
| 4 | 北京 | 108742.07 | 15 | 陕西 | -26834.21 | 26 | 新疆 | -60509.42 |
| 5 | 山东 | 104980.21 | 16 | 江西 | -32836.87 | 27 | 甘肃 | -64853.00 |
| 6 | 上海 | 69186.26 | 17 | 重庆 | -35511.41 | 28 | 海南 | -87831.39 |
| 7 | 四川 | 47848.98 | 18 | 山西 | -36033.23 | 29 | 宁夏 | -92681.43 |
| 8 | 河南 | 40297.66 | 19 | 天津 | -36300.20 | 30 | 青海 | -95186.63 |
| 9 | 河北 | 24156.47 | 20 | 广西 | -41645.87 | 31 | 西藏 | -100602.31 |
| 10 | 辽宁 | 11599.24 | 21 | 云南 | -42417.77 | |||
| 11 | 福建 | 8729.16 | 22 | 黑龙江 | -42739.20 |
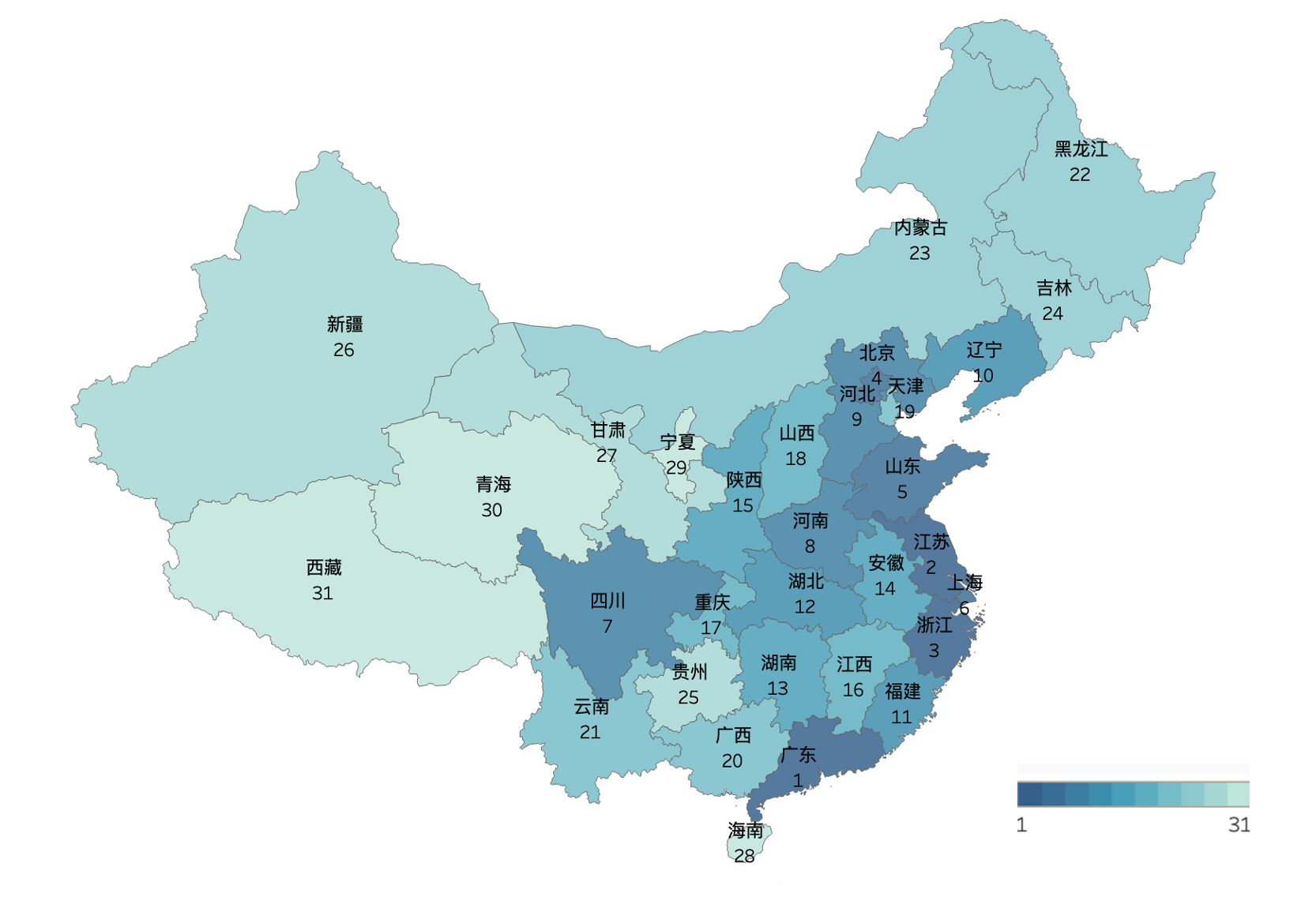
图14 我国各省普惠金融发展水平地图
注意,对于PCA算法笔者这里是将流程走了一遍,实际使用中也可以直接调包,sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False),参数如下:

结论分析
对于普惠金融的发展水平
笔者通过使用PCA方法和数据可视化方法对我国普惠金融发展水平进行综合评价,得到国各省普惠金融发展水平综合评价得分和我国各省普惠金融发展水平地图,创新了我国普惠金融发展水平评价方法。
普惠金融发展各省之间发展存在不均衡性。总的来看,以上海为中心的华东地区整体上普惠金融发展水平相对较高,其次是以北京为中心的京津地区,广东省在华南地区独树一帜,而四川省在西部地区明显高出一筹。整体上讲,华南和西部地区普惠金融发展水平相对较低。
基于文献调研,相较于传统的实证分析,使用PCA方法进行综合评价创新了研究方法,可以从宏观上把握评价水平,但是由于缺少具体各个指标的回归系数,较难提出针对性的建议。
对于PCA算法
本项目笔者只是实现了最基本的PCA 算法,由于实验数据只有9个维度,所以基本的PCA算法也基本满足了条件,但是在PCA降维中,需要计算样本协方差矩阵 的最大 个特征向量,再将其排序、组成矩阵得到低维投影。倘若样本量太多,样本特征过多,会导致协方差矩阵 计算量变得很大,效率低下。
对于效率问题,一种方法是使用SVD分解协方差矩阵,传统的PCA算法通过特征分解求解,而PCA算法也可以通过SVD来完成。事实上,scikit-learn的PCA算法就是用SVD分解,而不是特征值分解。在不求解协方差矩阵的情况下,得到右奇异矩阵V,即 PCA算法可以不通过特征分解,而是采用SVD方法,这个方法在样本量很大的时候很有效。
还可以结合GBDT算法:基于改进主成分分析法的特征约简算法,结合数据挖掘,引入GBDT算法进行维度缩减。针对具有高阶相关性的属性特征,或属性主特征的非正交方向上有多个方差较大的情况下,PCA算法的属性约简性能会大大降低。因此,引入GBDT算法更新PCA算法的初始输入,在GBDT算法多参数的干预下实现数据个性化预处理,降低样本属性特征的高阶相关性,从而快速计算得到方差较大的方向向量,实现样本属性约简。
源代码
源文件可以在笔者的Github下载:
├── PCA code.ipynb
├── PCA_finance2.xlsx
└── 普惠金融发展水平评价指标原始数据.xlsx
[1] 焦瑾璞,黄亭亭,汪天都,张韶华,王瑱.中国普惠金融发展进程及实证研究[J].上海金融,2015(04):12-22.DOI:10.13910/j.cnki.shjr.2015.04.003.
[2] 魏厦.河北省科技竞争力评价研究——基于主成分分析[J].调研世界,2019(06):45-48.DOI:10.13778/j.cnki.11-3705/c.2019.06.008.
[3] 于晓虹,楼文高,余秀荣.中国省际普惠金融发展水平综合评价与实证研究[J].金融论坛,2016,21(05):18-32.DOI:10.16529/j.cnki.11-4613/f.2016.05.003.