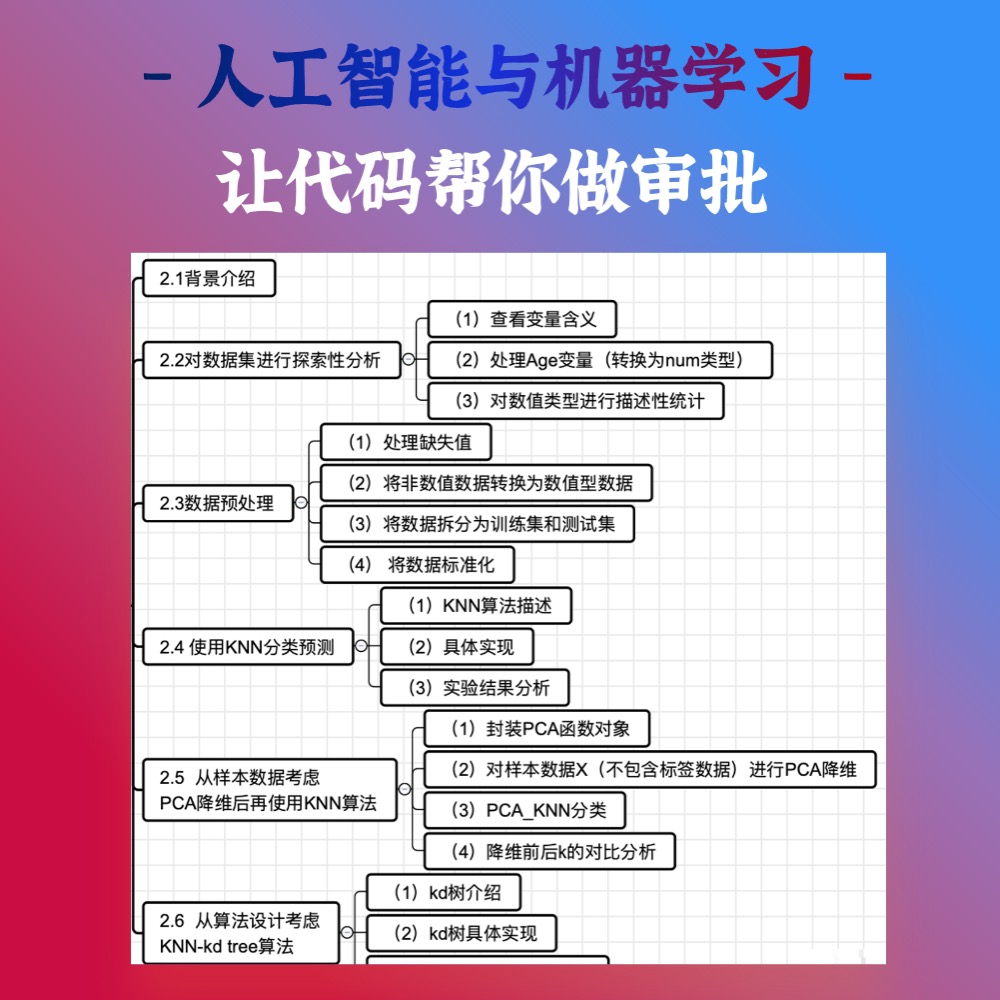
本实验笔者将尝试使用Gram-Schmidt正交化（CGS+MGS）和Householder（自编HS+Matlab qr）方法进行QR分解，并对比分析不同方法的稳定性，同时使用QR分解方法求矩阵的逆。思维导图如下：

—– 源文件可以在笔者的 [Github下载](https://github.com/fubostudy/Optimal-Method/tree/main/Matlab%E5%AE%9E%E7%8E%B0QR%20%E5%88%86%E8%A7%A3%20(Gram%E2%80%93Schmidt%26%20Householder%EF%BC%89) ├── A.mat ├── B.mat ├── Matlab实现QR 分解 (Gram–Schmidt& Householder）.pdf ├── QRcode.m ├── backsub.m └── invB.xlsx