【如何衡量金融风险】通过Python实现参数法、蒙特卡洛法及历史数据法计算期货产品的VaR和ES
|
1,742
|
金融&管理

2491 字
|
44 分钟

本文对金融风险管理和金融基础设施建设课程进行结合实践，选取了 Heng Seng Index Futures(HSIF)、Hang Seng China Enterprises Index Futures(HHIF)和Tencent Holdings Ltd. Futures(TCHF)三只期货产品从2016-06-01 —— 2022-06-01的历史数据，通过python实现参数法、蒙特卡洛法及历史数据法计算期货产品在95%置信度下的VaR和ES（CVaR）。

题目说明

针对①HSI Index futures, ②其他任意一个 Index futures, ③其他任意一个 Stock futures

  1. 使用参数法、蒙特卡洛法及历史数据法计算该期货产品在95%置信度下的VaR

  2. 计算该期货产品在95%置信度下的CvaR/ES

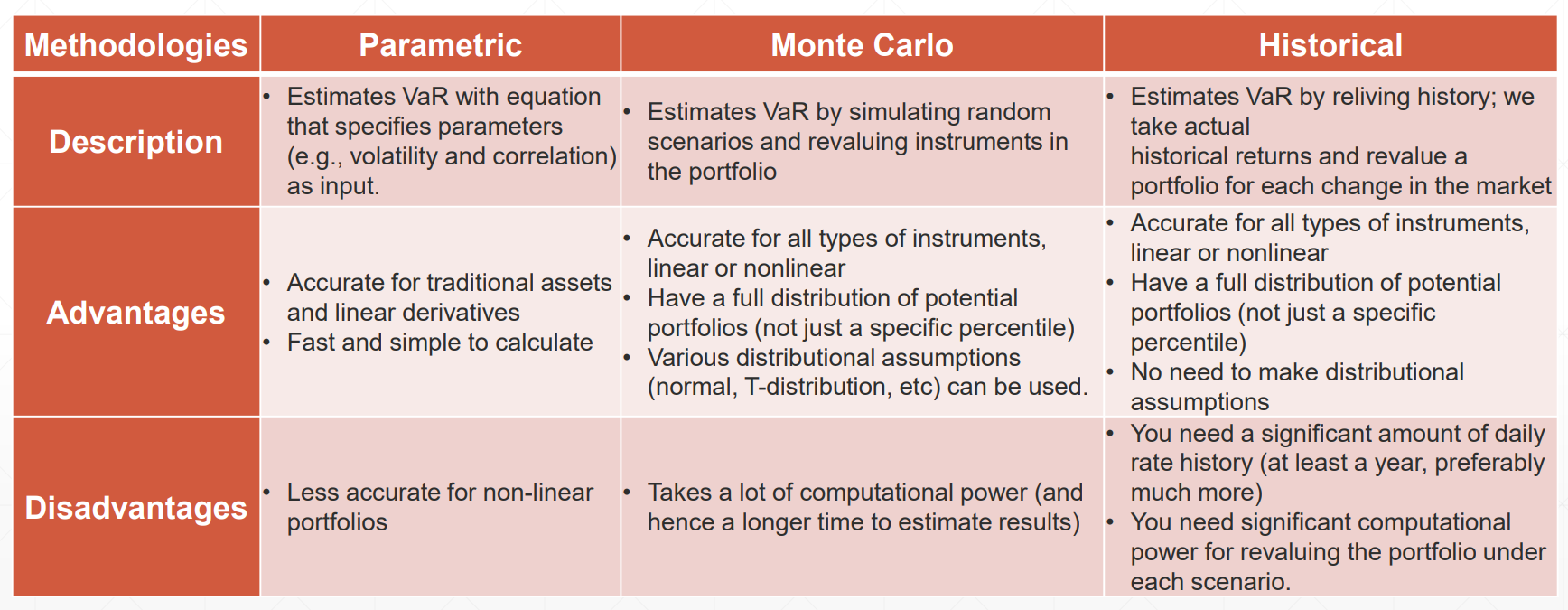
表格 描述已自动生成

图1：计算方法

数据探索

数据来源

笔者这里选取的数据说明如下：

  • 选取的Futrues
    • Heng Seng Index Futures(HSIF)
    • Hang Seng China Enterprises Index Futures(HHIF)
    • Tencent Holdings Ltd. Futures(TCHF)
  • 截取数据时段：2016-06-01 —— 2022-06-01

  • 数据来源：Wind数据库
  • 编程环境：Python3 + Jupyter Notebook

数据基本情况

首先导入python在Jupyter Notebook 环境中需要使用到的包

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn
%matplotlib inline

下图2、图3、图4分别是HSIF、HHIF、TCHF的数据列表，从中可以看到期货历史数据的基本情况。其中，日期、收盘价、涨跌幅是关键指标。

HSIF = pd.read_excel('/Users/fubo/Desktop/HSIF.xlsx')
HSIF

img

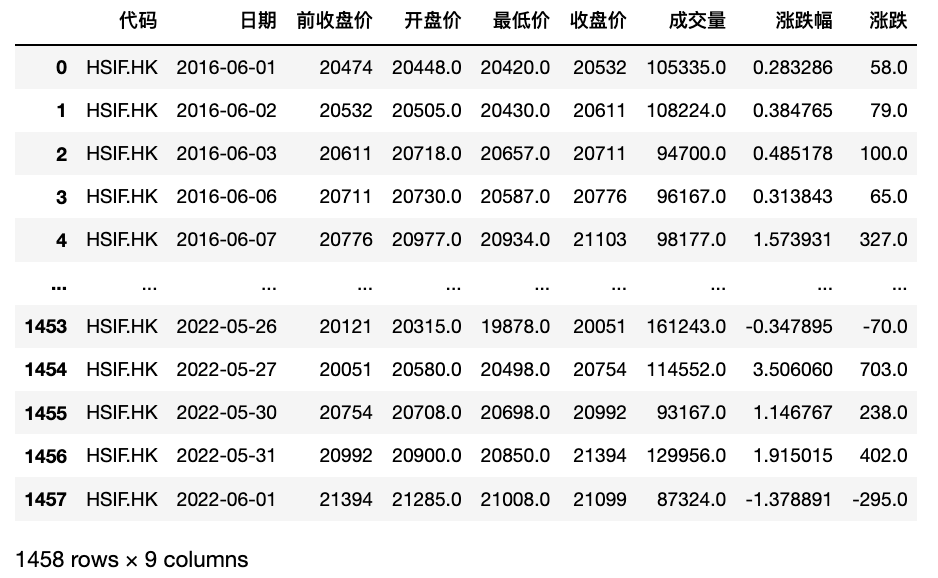
图2: HSIF数据基本情况

HHIF = pd.read_excel('/Users/fubo/Desktop/HHIF.xlsx')
HHIF

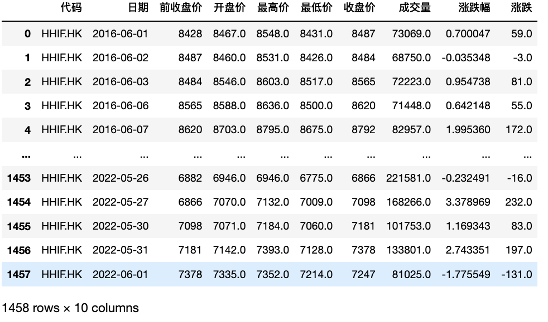
图3: HHIF数据基本情况

TCHF = pd.read_excel('/Users/fubo/Desktop/TCHF.xlsx')
TCHF

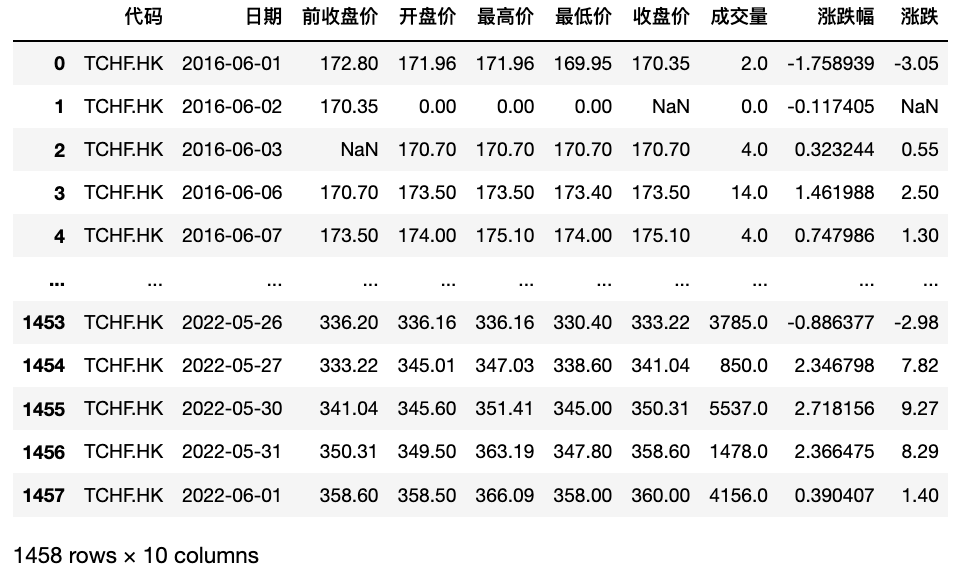
表格 描述已自动生成

图4: TCHF数据基本情况

期货日价格（收盘价）走势图

​ 接下来笔者使用期货的日收盘价对期货产品的价格变动趋势进行可视化，从下图5、图6、图7可以看到期货价格走势。

HSIF1 = HSIF.rename(index=HSIF['日期'])
plt.figure(figsize=(12, 8))
plt.plot(HSIF1['收盘价'].dropna())
plt.show

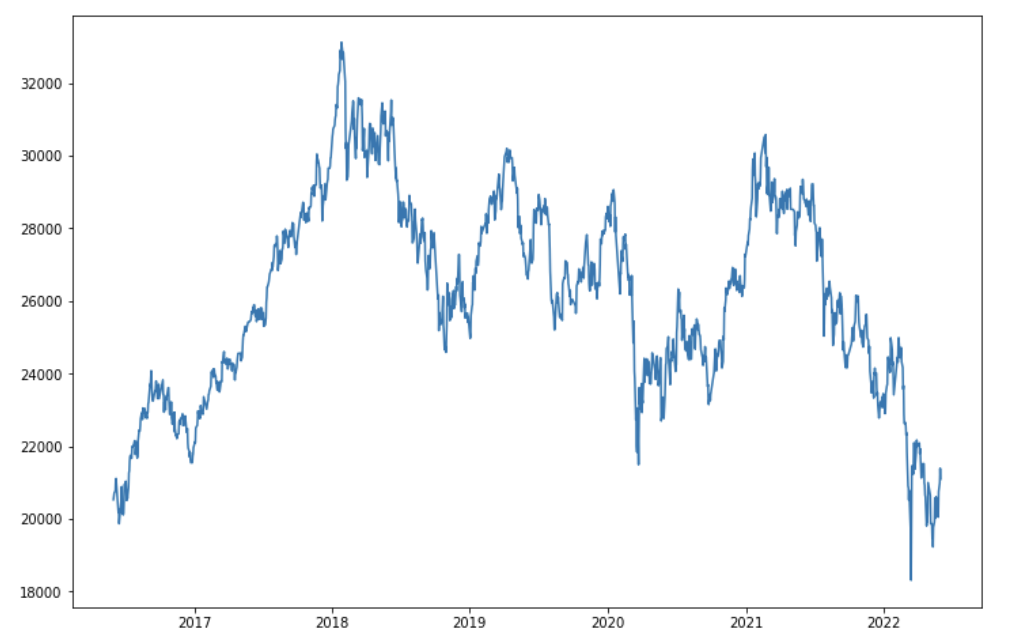
图表, 折线图 描述已自动生成

图5: HSIF走势图

HHIF1 = HHIF.rename(index=HHIF['日期'])
plt.figure(figsize=(12, 8))
plt.plot(HHIF1['收盘价'].dropna())
plt.show

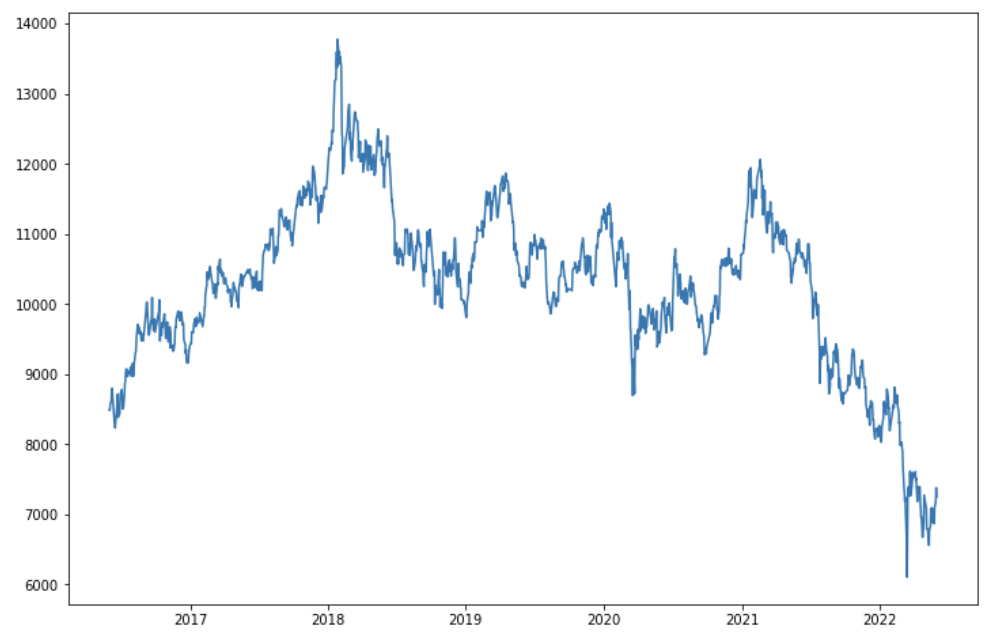
图表 描述已自动生成

图6: HHIF走势图

TCHF1 = TCHF.rename(index=TCHF['日期'])
plt.figure(figsize=(12, 8))
plt.plot(TCHF1['收盘价'].dropna())
plt.show

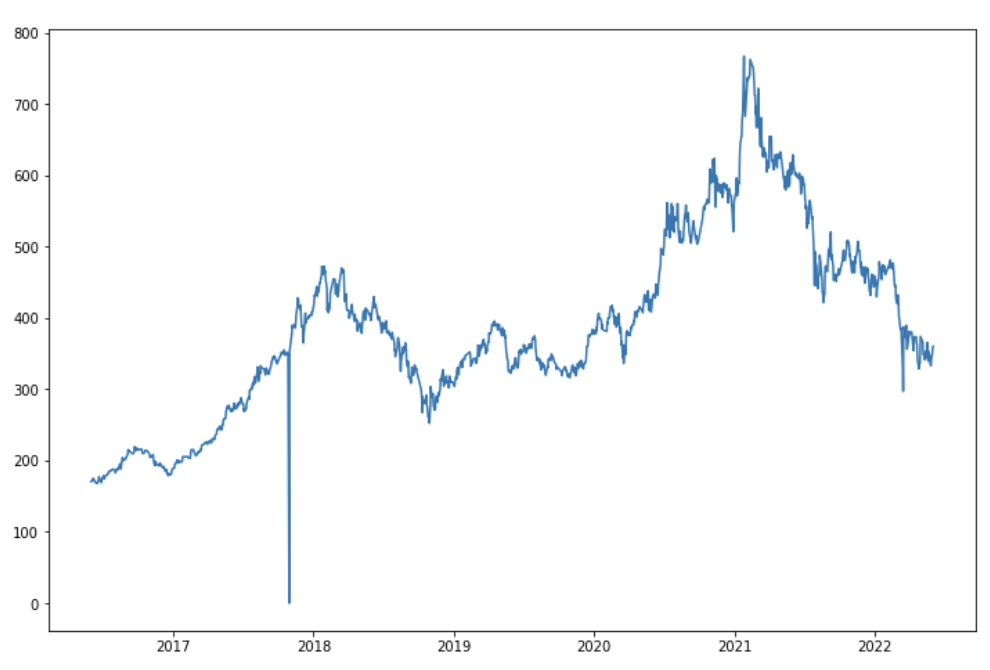
图表, 折线图 描述已自动生成

图7: TCHF走势图

期货日收益率频率分布直方图

如图8、9、10是HSIF、HHIF、TCHF的日收益频率分布直方图，从中可以看到大致都服从正态分布。

对于蒙特卡洛法与参数法而言，当抽样样本足够大时，如果二者的结果完全相等，则说明原数据完全服从正态分布，越接近正态分布的假设越强。

plt.figure(figsize= (8,6))
HSIF['涨跌幅'].hist(bins=50, alpha=0.6, color='steelblue', edgecolor='k')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

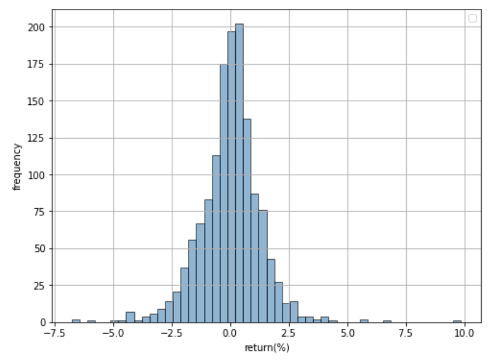
图8: HSIF日收益率频率分布直方图

plt.figure(figsize= (8,6))
HHIF['涨跌幅'].hist(bins=50, alpha=0.6, color='violet',edgecolor='k')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

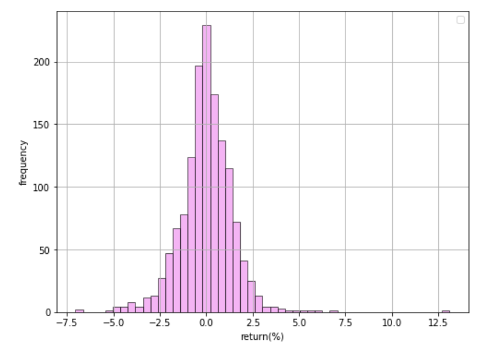
图9: HHIF日收益率频率分布直方图

plt.figure(figsize= (8,6))
TCHF['涨跌幅'].hist(bins=50, alpha=0.6, color='springgreen',edgecolor='k')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

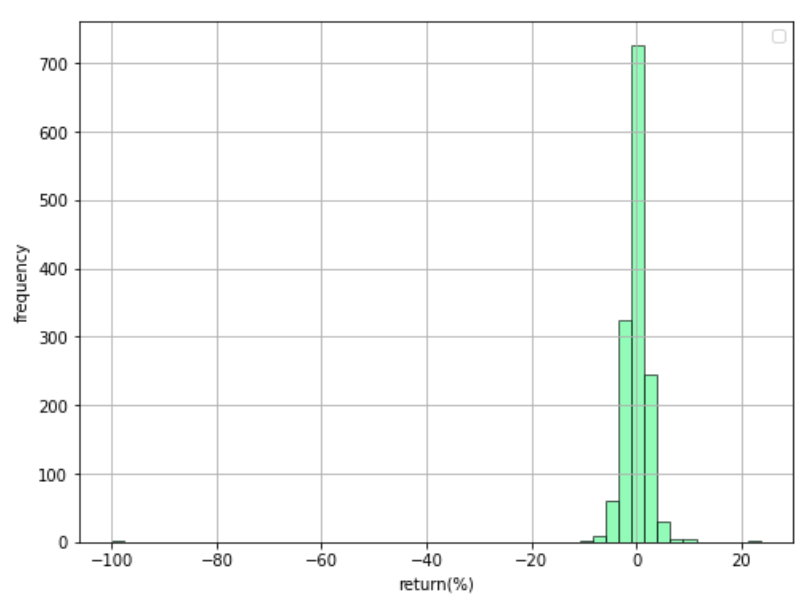
图表 描述已自动生成

图10: TCHF日收益率频率分布直方图

期货累计收益率走势图

下图11是HSIF、HHIF、TCHF的累计收益率走势图。

HSIF['累计收益率'] = HSIF['涨跌幅'].cumsum()
HHIF['累计收益率'] = HHIF['涨跌幅'].cumsum()
TCHF['累计收益率'] = TCHF['涨跌幅'].cumsum()
df1 = pd.DataFrame(data=[HSIF['累计收益率'],HHIF['累计收益率'],TCHF['累计收益率']])
df2 = pd.DataFrame(df1.values.T, index=df1.columns, columns=df1.index)
df2.columns = ['HSIF','HHIF','TCHF']
df2=df2.rename(index=HHIF['日期'])
HSIF['累计收益率'] = HSIF['涨跌幅'].cumsum()
HHIF['累计收益率'] = HHIF['涨跌幅'].cumsum()
TCHF['累计收益率'] = TCHF['涨跌幅'].cumsum()
df1 = pd.DataFrame(data=[HSIF['累计收益率'],HHIF['累计收益率'],TCHF['累计收益率']])
df2 = pd.DataFrame(df1.values.T, index=df1.columns, columns=df1.index)
df2.columns = ['HSIF','HHIF','TCHF']
df2=df2.rename(index=HHIF['日期'])

plt.figure(figsize=(12, 8))
plt.title('Cumulative Returns')
plt.plot(df2)
plt.legend(labels=['HSIF','HHIF','TCHF'])
plt.show

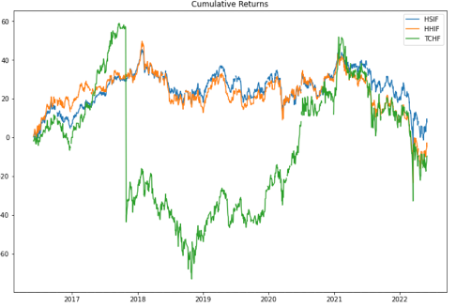
图11: HSIF、HHIF、TCHF的累计收益率走势图

计算期货在 95%置信度下的VaR/ CVaR（ES）

VaR（Value at Risk），即在险价值；CVaR（Conditional Value at risk），即条件在险价值，又被称作ES（Expected Shortfall）。笔者在下面的计算都统称为VaR和ES。

参数法

​ 参数法的计算公式如下：

\mathrm{VaR}=\mu-\sigma Y

\mathrm{ES}=\mu-\sigma \frac{e^{-Y^{2} / 2}}{\sqrt{2 \pi}(1-X)}

, where ? is the confidence level and Y=N^{-1}(X)

​ 由上2.4知三只期货产品的日回报数据都近似服从正态分布，因此原数据的平均和方差近似正态分布的均值和方差。

笔者这里直接使用Python的scipy库进行计算，以HSIF为例，代码如下：

# HSIF
from scipy.stats import norm
mean_return_HSIF = HSIF['涨跌幅'].mean()
std_HSIF = HSIF['涨跌幅'].std()

Y95 = norm.ppf(0.95)

HSIF_VaR_95_p = mean_return_HSIF - norm.ppf(0.95)*std_HSIF
HSIF_ES_95_p = mean_return_HSIF - std_HSIF * np.exp(-pow(Y95,2) / 2) / pow(2 * np.pi,0.5) / 0.05

print(HSIF_VaR_95_p,HSIF_ES_95_p)

根据上述VaR和ES的计算公式，计算结果为：

HSIF_VaR_95_p = -2.1328242921358087

HSIF_ES_95_p = -2.676122627831071

因此，HSIF的VaR为2.13% ，ES（CVaR）为2.68% 。

同理，HHIF的计算结果为：

#HHIF
mean_return_HHIF = HHIF['涨跌幅'].mean()
std_HHIF = HHIF['涨跌幅'].std()
HHIF_VaR_95_p = mean_return_HHIF - norm.ppf(0.95)*std_HHIF
HHIF_ES_95_p = mean_return_HHIF - std_HHIF * np.exp(-pow(Y95,2) / 2) / pow(2 * np.pi,0.5) / 0.05
print(HHIF_VaR_95_p,HHIF_ES_95_p)

HHIF_VaR_95_p = -2.3466696292222493

HHIF_ES_95_p = -2.9420088105744453

因此，HHIF的VaR为2.35% ，ES（CVaR）为2.94% 。

同理，TCHF的计算结果为：

#TCHF
mean_return_TCHF = TCHF['涨跌幅'].mean()
std_TCHF = TCHF['涨跌幅'].std()
TCHF_VaR_95_p = mean_return_TCHF - norm.ppf(0.95)*std_TCHF
TCHF_ES_95_p = mean_return_TCHF - std_TCHF * np.exp(-pow(Y95,2) / 2) / pow(2 * np.pi,0.5) / 0.05
print(TCHF_VaR_95_p,TCHF_ES_95_p)

TCHF_VaR_95_p = -5.722884557482017

TCHF_ES_95_p = -7.1749958410381955

因此，TCHF的VaR为5.72% ，ES（CVaR）为7.17% 。

蒙特卡洛法

原理

关于蒙特卡洛模拟的原理, 假设股票价格波动符合几何布朗运动:

S_{t}=S_{t-1}+S_{t-1}(\mu d t+\varepsilon \sqrt{d t})

S_{t} 是今天股票的价格, S_{t-1} 是前一天的股票价格, \mu 是股票每天的收益率的均值, \varepsilon 是服从标准正态 分布的随机项, d t 是模拟的时间间隔, 如每天模拟一次股票价格, 则 d t=1, 如每天模拟两次, 则 d t= 0.5 。

基于上述计算公式，笔者首先使用python定义一个函数：GBM(s_0, mu, sigma, T, n)，用于计算一次几何布朗运动的价格数据：

#蒙特卡洛模拟法
# 定义一个函数，用于计算一次几何布朗运动的价格数据
def GBM(s_0, mu, sigma, T, n):
    """ 计算几何布朗运动的期货价格数据
    parameters:
    s_0:开始价格
    mu:观察期日收益率的均值
    sigma:观察期日收益率的标准差
    T:预测价格的周期长度，如预测下一天，T=1, 预测10天，T=10;
    n:单次模拟的步数，步数越大，模拟得越精确
    """
    # 计算delta_t
    delta_t = T/n
    # 创建一个空的列表用于储存价格数据
    simulated_price = [s_0]
    # 模拟价格走势
    for i in range(n):
        # 获取期初价格
        start_price = simulated_price[i]
        # 按照标准正态分布产生一个随机数
        epsilon = np.random.normal()
        # 根据几何布朗运动公式计算期末价格
        end_price = start_price + start_price * (mu*delta_t + sigma*epsilon*np.sqrt(delta_t))
        # 价格应大于0
        end_price = max(0, end_price)  
        # 将算的的结果存入列表
        simulated_price.append(end_price)

    return simulated_price

同时，定义一个计算ES的函数：

# 计算ES的函数
def ES_daily(a,x):
    VaR=np.percentile(a.dropna(),100-x)
    ES=a[a<=VaR].mean()
    return ES

HSIF

接下来笔者仍然以HSIF为例，说明使用蒙特卡洛法计算期货VaR和ES的具体方法。

首先使用蒙特卡洛法产生10000个1天的模拟价格，取出它们的最终价格，并保存在simulated_prices_1空列表中。具体方法如下：用昨天的股票数据作为起始数据，用历史数据的每天的平均收益率和波动率代入公式模拟一天后的股票价格10000次，就得到10000个收益率数据。

# 产生10000个1天的模拟价格，取出它们的最终价格，并保存在simulated_prices_1空列表中
simulated_prices_1 = []
s_0 = HSIF['收盘价'][1457]
mu_1 =mean_return_HSIF
sigma_1 = std_HSIF
for i in range(10000):
    # 模拟一次几何布朗运动
    simulated_price = GBM(s_0, mu_1, sigma_1, 1,100)
    # 取出最终价格
    final_price = simulated_price[-1]
    simulated_prices_1.append(final_price)

simulated_prices_11 = pd.DataFrame(simulated_prices_1)
simulated_return_1 = np.log(simulated_prices_11/simulated_prices_11.shift(1))

#--------------------------------------------

#HSIF
simulated_return_1.hist(bins=50, alpha=0.6, color='steelblue',edgecolor='k')
HSIF_VaR_95_mcs = np.percentile(simulated_return_1.dropna(), 5)
HSIF_ES_95_mcs = float(ES_daily(simulated_return_1.dropna(),95))
print(HSIF_VaR_95_mcs,HSIF_ES_95_mcs)


plt.axvline(HSIF_VaR_95_mcs, color='r', linewidth=1,label = 'HSIF_VaR_95_mcs')
plt.axvline(HSIF_ES_95_mcs, color='m', linewidth=1,label = 'HSIF_ES_95_mcs')
plt.legend()
plt.title('Monte Carlo_HSIF')
plt.grid()
plt.xlabel('return(%)')
plt.ylabel('frequency')

再对这10000个收益率从大到小进行排序，通过np.percentile()函数取95%的分位数，则可得到95%的VaR。再定义ES_daily(a,x)函数，对排序前5%的所有收益率求期望值，则可得到95%的ES。计算结果为：

HSIF_VaR_95_mcs = -3.1230316842764667

HSIF_ES_95_mcs = -3.927497819671775

因此，HSIF的VaR为3.12% ，ES（CVaR）为3.93% 。

蒙特卡洛模拟 HSIF 日收益额直方图如图12所示：

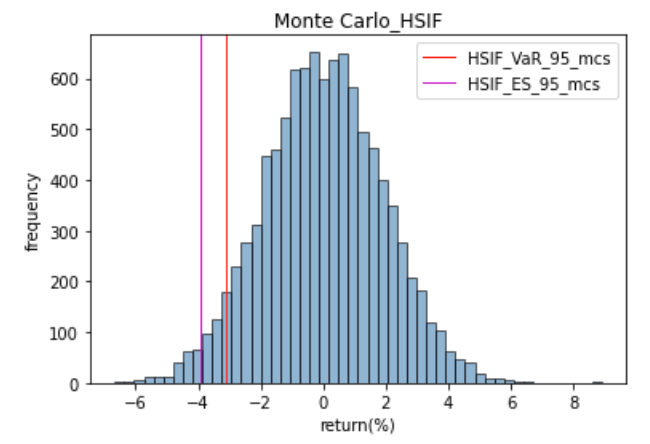
图12：蒙特卡洛模拟 HSIF 日收益额直方图

HHIF

同理，HHIF的计算结果为：

# 产生10000个1天的模拟价格，取出它们的最终价格，并保存在simulated_prices_1空列表中
simulated_prices_1 = []
s_0 = HHIF['收盘价'][1457]
mu_1 =mean_return_HHIF
sigma_1 = std_HHIF
for i in range(10000):
    # 模拟一次几何布朗运动
    simulated_price = GBM(s_0, mu_1, sigma_1, 1,100)
    # 取出最终价格
    final_price = simulated_price[-1]
    simulated_prices_1.append(final_price)

simulated_prices_11 = pd.DataFrame(simulated_prices_1)
simulated_return_1 = np.log(simulated_prices_11/simulated_prices_11.shift(1))

#--------------------------------------------
#HHIF

simulated_return_1.hist(bins=50, alpha=0.6, color='violet',edgecolor='k')
HHIF_VaR_95_mcs = np.percentile(simulated_return_1.dropna(), 5)
HHIF_ES_95_mcs = float(ES_daily(simulated_return_1.dropna(),95))
print(HHIF_VaR_95_mcs,HHIF_ES_95_mcs)

plt.axvline(HHIF_VaR_95_mcs, color='r', linewidth=1,label = 'HHIF_VaR_95_mcs')
plt.axvline(HHIF_ES_95_mcs, color='m', linewidth=1,label = 'HHIF_ES_95_mcs')
plt.legend()
plt.title('Monte Carlo_HHIF')
plt.grid()
plt.xlabel('return(%)')
plt.ylabel('frequency')

HHIF_VaR_95_mcs = -3.4363784036506324

HHIF_ES_95_mcs = -4.274287672223244

因此，HHIF的VaR为3.44% ，ES（CVaR）为4.27% 。

蒙特卡洛模拟 HHIF日收益额直方图如图13所示：

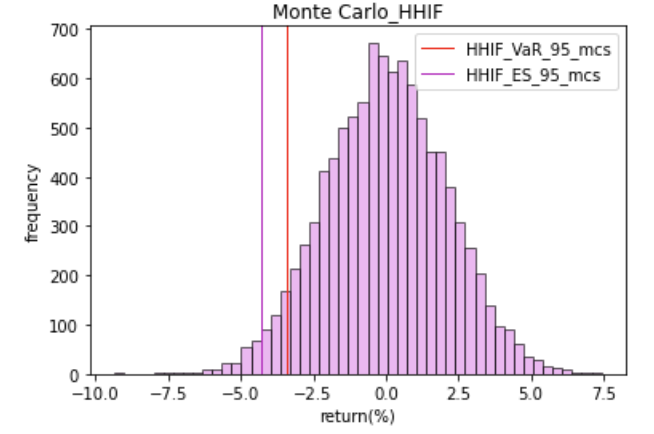
图表, 直方图 描述已自动生成

图13：蒙特卡洛模拟 HHIF 日收益额直方图

TCHF

同理，TCHF的计算结果为：

# 产生10000个1天的模拟价格，取出它们的最终价格，并保存在simulated_prices_1空列表中
simulated_prices_2 = []
s_0 = TCHF['收盘价'][1457]
mu_1 =mean_return_TCHF
sigma_1 = std_TCHF
for i in range(10000):
    # 模拟一次几何布朗运动
    simulated_price = GBM(s_0, mu_1, sigma_1, 1,100)
    # 取出最终价格
    final_price = simulated_price[-1]
    simulated_prices_2.append(final_price)

simulated_prices_11 = pd.DataFrame(simulated_prices_2)
simulated_return_2 = np.log(simulated_prices_11/simulated_prices_11.shift(1))

#--------------------------------------------

#TCHF
simulated_return_2[np.isfinite(simulated_return_2)].hist(bins=50, alpha=0.6, color='springgreen',edgecolor='k')
TCHF_VaR_95_mcs = np.percentile(simulated_return_1.dropna(), 5)
TCHF_ES_95_mcs = float(ES_daily(simulated_return_2[np.isfinite(simulated_return_2)].dropna(),95))
print(TCHF_VaR_95_mcs,TCHF_ES_95_mcs)

plt.axvline(TCHF_VaR_95_mcs, color='r', linewidth=1,label = 'TCHF_VaR_95_mcs')
plt.axvline(TCHF_ES_95_mcs, color='m', linewidth=1,label = 'TCHF_ES_95_mcs')
plt.legend()
plt.title('Monte Carlo_TCHF')
plt.grid()
plt.xlabel('return(%)')
plt.ylabel('frequency')

TCHF_VaR_95_mcs = -3.4363784036506324

TCHF_ES_95_mcs = -12.45751691251197

因此，TCHF的VaR为3.44% ，ES（CVaR）为12.46% 。

蒙特卡洛模拟 TCHF 日收益额直方图如图14所示：

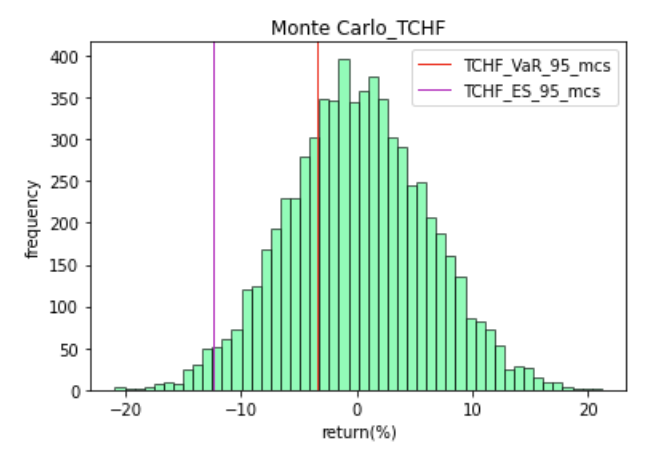
图表, 直方图 描述已自动生成

图14：蒙特卡洛模拟 TCHF 日收益额直方图

历史数据法

​ 对三只期货从2016-06-01 到 2022-06-01的历史数据从小到大排序，并分别选取排序在第5%的点作为VaR；选取前5%的点的期望值作为ES。代码如下：

#HSIF
HSIF_VaR_95_h = np.percentile(HSIF['涨跌幅'].dropna(), 5)
HSIF_ES_95_h = ES_daily(HSIF['涨跌幅'],95)
print(HSIF_VaR_95_h,HSIF_ES_95_h)

HSIF的计算结果如下：

HSIF_VaR_95_h = -2.0673545164652247

HSIF_ES_95_h = -3.02709750262999

因此，HSIF的VaR为2.07% ，ES（CVaR）为3.03% 。

HHIF的计算结果如下：

#HHIF
HHIF_VaR_95_h =np.percentile(HHIF['涨跌幅'].dropna(), 5)
HHIF_ES_95_h = ES_daily(HHIF['涨跌幅'],95)
print(HHIF_VaR_95_h,HHIF_ES_95_h)

HHIF_VaR_95_h = -2.2626761171932657

HHIF_ES_95_h = -3.2903785263969985

因此，HSIF的VaR为2.26% ，ES（CVaR）为3.29% 。

TCHF的计算结果如下：

#TCHF
TCHF_VaR_95_h =np.percentile(TCHF['涨跌幅'].dropna(), 5)
TCHF_ES_95_h = ES_daily(TCHF['涨跌幅'],95)
print(TCHF_VaR_95_h,TCHF_ES_95_h)

TCHF_VaR_95_h = -3.434924218052804

TCHF_ES_95_h = -6.167645465180926

因此，HSIF的VaR为3.43% ，ES（CVaR）为6.17% 。

总结

VaR对比

笔者对三只期货的使用三种不同的方法得到的VaR（图15、16、17）和ES结果（图18、19、20）进行对比分析:

# HSIF:VaR对比
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
plt.figure(figsize= (8,6))
HSIF['涨跌幅'].hist(bins=50, alpha=0.6, color='steelblue', edgecolor='k')
plt.axvline(HSIF_VaR_95_h, color='r', linewidth=1,label = 'HSIF_VaR_95_h')
plt.axvline(HSIF_VaR_95_p, color='g', linewidth=1,label = 'HSIF_VaR_95_p')
plt.axvline(HSIF_VaR_95_mcs, color='k', linewidth=1,label = 'HSIF_VaR_95_mcs')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

img

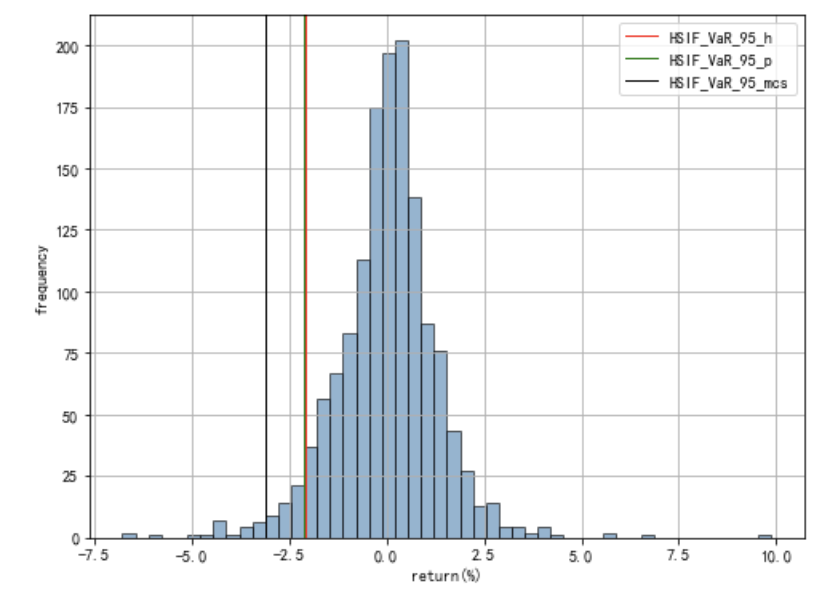
图15: HSIF:VaR对比

# HHIF:VaR对比
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
plt.figure(figsize= (8,6))
HHIF['涨跌幅'].hist(bins=50, alpha=0.6, color='violet', edgecolor='k')
plt.axvline(HHIF_VaR_95_h, color='r', linewidth=1,label = 'HHIF_VaR_95_h')
plt.axvline(HHIF_VaR_95_p, color='g', linewidth=1,label = 'HHIF_VaR_95_p')
plt.axvline(HHIF_VaR_95_mcs, color='k', linewidth=1,label = 'HHIF_VaR_95_mcs')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

img

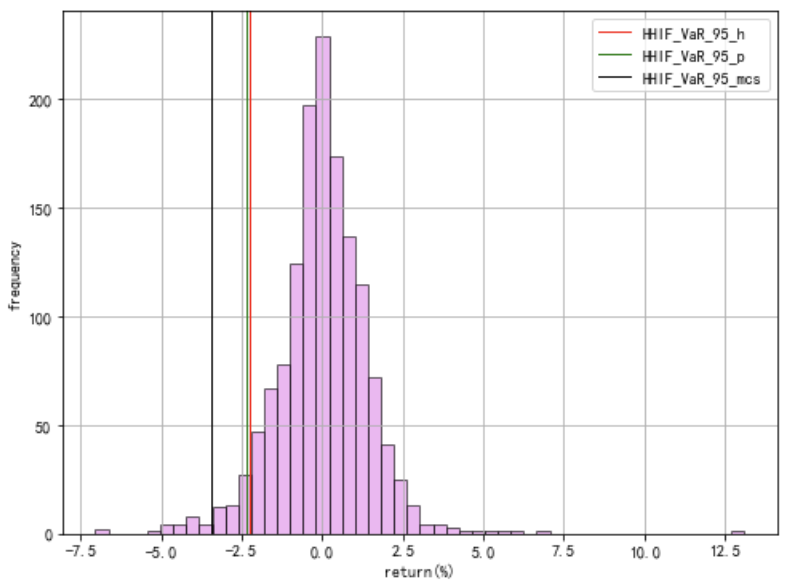
图16: HHIF:VaR对比

# TCHF:VaR对比
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
plt.figure(figsize= (8,6))
TCHF['涨跌幅'].hist(bins=50, alpha=0.6, color='springgreen', edgecolor='k')
plt.axvline(TCHF_VaR_95_h, color='r', linewidth=1,label = 'TCHF_VaR_95_h')
plt.axvline(TCHF_VaR_95_p, color='g', linewidth=1,label = 'TCHF_VaR_95_p')
plt.axvline(TCHF_VaR_95_mcs, color='k', linewidth=1,label = 'TCHF_VaR_95_mcs')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

img
图17: TCHF:VaR对比

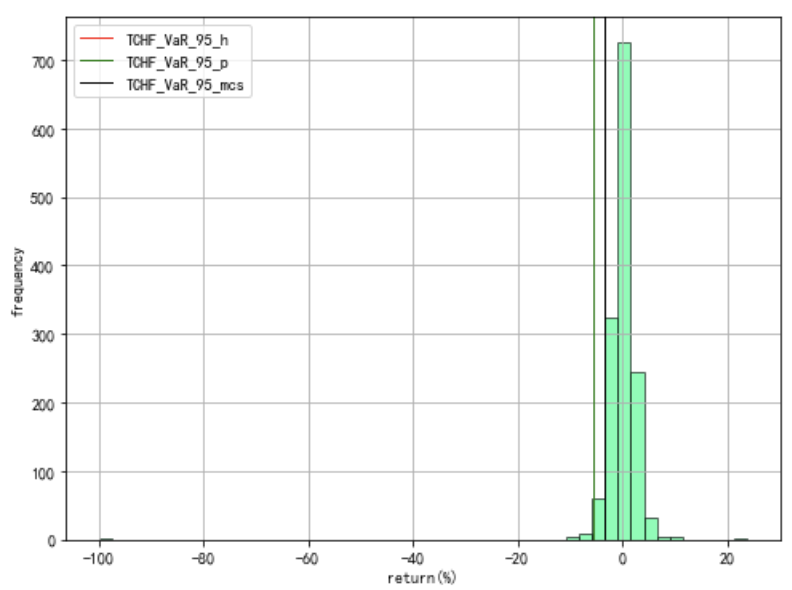
ES对比

# HSIF:ES对比
from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
plt.figure(figsize= (8,6))
HSIF['涨跌幅'].hist(bins=50, alpha=0.6, color='steelblue', edgecolor='k')
plt.axvline(HSIF_ES_95_h, color='r', linewidth=1,label = 'HSIF_ES_95_h')
plt.axvline(HSIF_ES_95_p, color='m', linewidth=1,label = 'HSIF_ES_95_p')
plt.axvline(HSIF_ES_95_mcs, color='k', linewidth=1,label = 'HSIF_ES_95_mcs')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

img

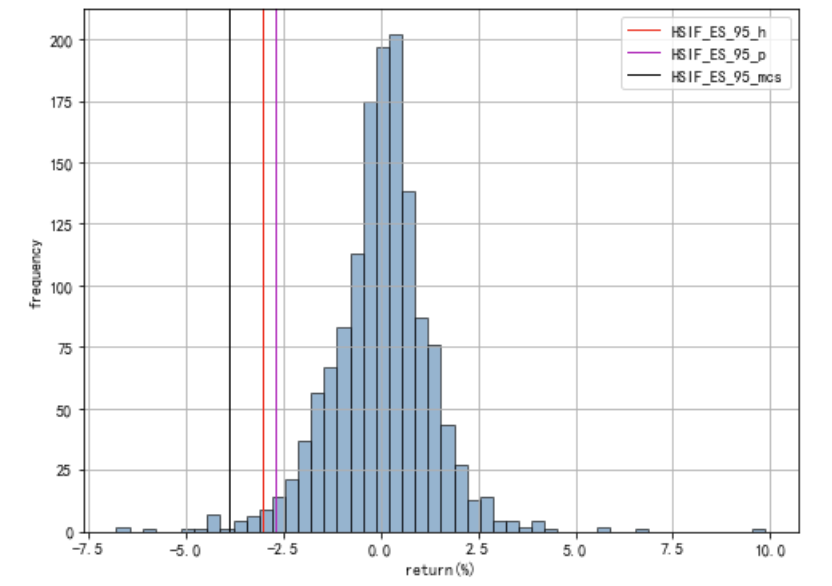
图18: HSIF:ES对比

from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
plt.figure(figsize= (8,6))
HHIF['涨跌幅'].hist(bins=50, alpha=0.6, color='violet', edgecolor='k')
plt.axvline(HHIF_ES_95_h, color='r', linewidth=1,label = 'HHIF_ES_95_h')
plt.axvline(HHIF_ES_95_p, color='m', linewidth=1,label = 'HHIF_ES_95_p')
plt.axvline(HHIF_ES_95_mcs, color='k', linewidth=1,label = 'HHIF_ES_95_mcs')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

img

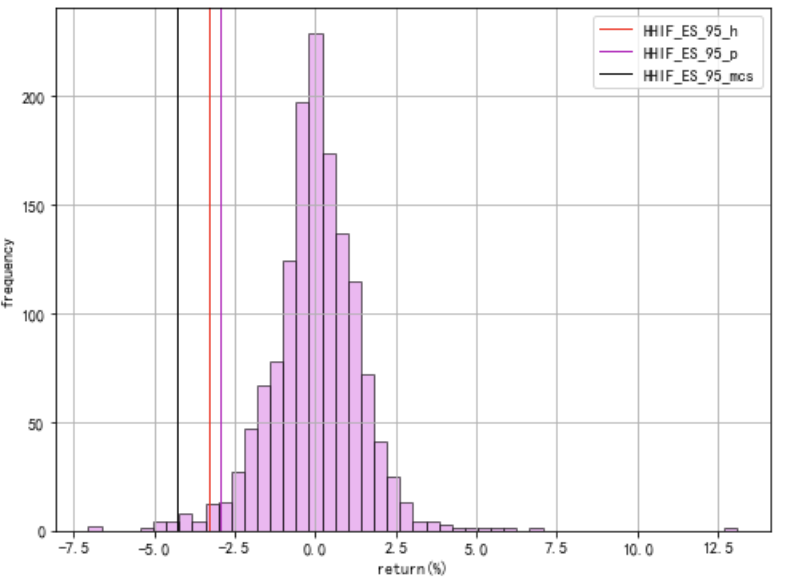
图19: HHIF:ES对比

from pylab import mpl
mpl.rcParams['font.sans-serif']=['SimHei']
mpl.rcParams['axes.unicode_minus']=False
plt.figure(figsize= (8,6))
TCHF['涨跌幅'].hist(bins=50, alpha=0.6, color='springgreen', edgecolor='k')
plt.axvline(TCHF_ES_95_h, color='r', linewidth=1,label = 'TCHF_ES_95_h')
plt.axvline(TCHF_ES_95_p, color='m', linewidth=1,label = 'TCHF_ES_95_p')
plt.axvline(TCHF_ES_95_mcs, color='k', linewidth=1,label = 'TCHF_ES_95_mcs')
plt.legend()
plt.xlabel('return(%)')
plt.ylabel('frequency')

图20: TCHF:ES对比

对比分析

进一步总结为表格，如图上述可视化表格，从表1、表2也可以看出：在VaR_95上，通过历史模拟法和参数法计算出来的VaR是比较相近的，特别是是对于HSIF和HHIF来说，使用蒙特卡洛模拟法计算出来的VaR值往往比其他的两种方法计算出来的VaR值要大。在ES_95上，计算出来的ES值，蒙特卡洛模拟法 > 历史模拟法 > 参数法。

表1: 期货产品在95%置信度下的VaR

VAR Parametric Monte Carlo Historical
HSIF 2.13% 3.12% 2.07%
HHIF 2.35% 3.44% 2.26%
TCHF 5.72% 3.44% 3.43%

表2: 期货产品在95%置信度下的ES（CvaR）

ES Parametric Monte Carlo Historical
HSIF 2.68% 3.93% 3.03%
HHIF 2.94% 4.27% 3.29%
TCHF 7.17% 12.46% 6.17%

ESpythonVaR金融风险管理
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																

							
							
						

																

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	









上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
【金融案例分析】GME游戏驿站：股票为何暴涨暴跌？是散户大战华尔街大鳄？阴谋论？还是正常市场行为？ 一文用金融原理进行趣味解读。

							
							

							
【我写了个小软件，老板说要给我加薪】微信助手｜个性化群发｜好友头像照片墙｜软件开发

							
							

							
【工具】pycharm使用指南（头文件、debug、macos快捷键）

							
							

							
【市场营销】宠物经济｜以3C、STP、4P框架分析智能宠物玩具Enabot进入中国的市场营销方案

							
							

							
【机器学习入门：K-Means聚类算法】Python实现手写数字图像分类｜PCA算法可视化｜MNIST数据集｜最优化方法分析

							
							

							
【金融案例分析】1987美国股灾（美国历史上的四大股灾、Portfolio Insurance、股指套利 、纽交所、DOT System）

							
							

							
【金融案例分析】Odd-Eighth Quotes（做市商报价spread、1997 Order Handling Rule）

							
							

							
【WeChatFriendTool】从0到1，从前端界面到后端接口，详解Python软件开发全过程。干货，看完小白也可以轻松写出一个软件！

							
							

							
【金融基建】如何计算期货或期货组合的保证金？

							
							

							
【金融基础设施建设｜三万字长文】证券交易机制(概述、金融产品、证券估值、证券交易机制、交易场所)

							
							

							
【论文数据|爬取与清洗】文本分析|数据清洗| Selenium 模拟登录与自动化下载|北大法宝网 Pkulaw 爬虫|天眼查爬虫| Charles抓包

							
							

							
【金融案例分析】香港恒生指数的发展历史（上市证券分类、香港金融市场上的重要节点、恒指的构成）

							
							

							
【如何用人工智能玩拼图游戏】八数码难题｜Python｜知识表示｜状态空间法｜深度优先算法｜广度优先算法｜无信息搜索｜启发式函数｜A*搜索算法

							
							

							
【金融案例分析】港交所的收市竞价尝试（CAS、U盘交易、汇丰秒杀门事件）

							
							

							
【《创新者的窘境》读书报告】何为破坏式创新？“创新者窘境”产生的原因？我们能否跳出创新者的窘境？

							
							

							
【论文修改｜审稿意见回复】数据分析：中国气候变化慈善基金中各主体的分布现状如何？公共部门｜私有部门｜第三方部门｜天眼查爬虫

							
							

							
【金融案例分析】深度解读：光大证券乌龙指事件是怎么回事？（套利交易、基金背后的金融原理，事件的过程与定性）

							
							

							
【Python 金融数据分析】使用PCA算法实现普惠金融发展水平的综合评价

							
							

							
【金融基础设施建设】概论（金融基础设施的定义、现状、国内外标准、基本特征、作用、风险）

							
							

							
【用机器学习建立银行信用卡自动审批分类器】KNN算法｜有监督分类算法｜金融数据分析｜UCI数据集

							
							

							
【如何让人工智能玩吃豆人游戏？】Pacman｜对抗博弈｜搜索策略｜minmax搜索算法｜alpha-beta 剪枝算法｜评估函数设计｜智能体

							
							

							
【创新管理】如何衡量一个区域的创新能力？—— 基于文献调研和数据分析的探索

							
							

							
【金融案例分析】阿姆斯特丹股票交易所的历史（世界上最早的永续债券&股票&股票基金、郁金香泡沫、荷兰皇家壳牌集团、东印度公司）

							
							

							
【Python爬虫——批量爬取北大法宝网(pkulaw)的法律判决书】看似简单的任务为何如此麻烦？Selenium破解滑块验证｜Xpath解析HTML｜Re正则表达式文本分析