本项目目的在于实现一种有监督分类算法,并应用于金融数据分析。笔者使用信用审批数据进行分析,使用机器学习构建一个像真实的银行一样的自动信用卡审批分类器。
完整地探索了数据预处理的过程,并且通过普通KNN算法(最高准确率为73.04%,k=3)、PCA降维后的KNN算法(最高准确率为74.35%,k=25)、KNN kd tree算法(最高准确率为87.39%,k=7)对此数据集进行对比分析和可视化。本项目的思维导图如下:
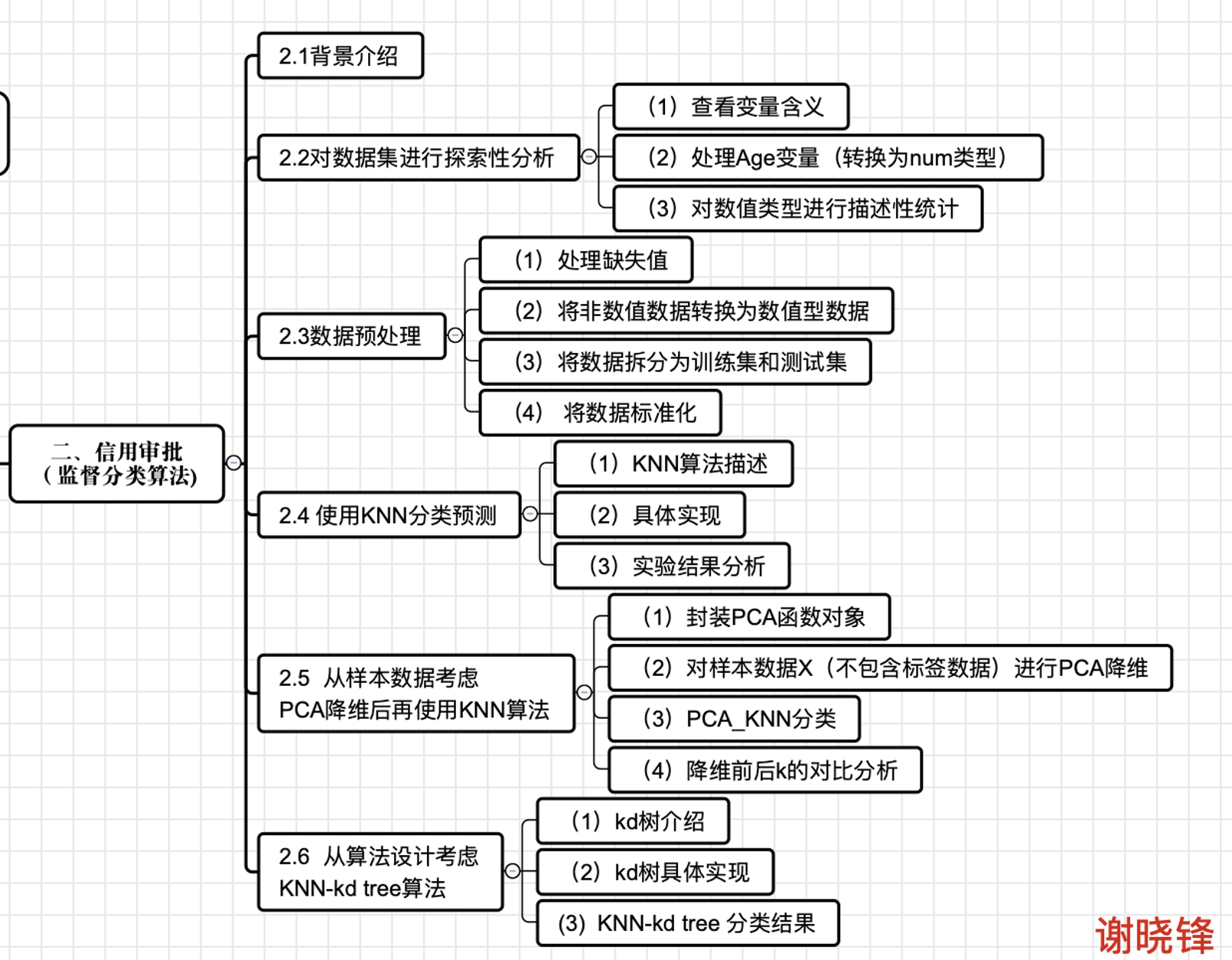
背景介绍
商业银行会收到很多信用卡申请,他们中的许多人会因为多种原因而被拒绝,例如有较高的贷款负债、较低的收入水平或较低的个人征信。如果靠人工手动分析这些信用卡申请,效率很低,容易出错且耗时,所以现在几乎每家商业银行都通过机器学习的进行自动化处理。在本次项目中,笔者将使用机器学习构建一个像真实的银行一样的自动信用卡审批分类器。
数据集探索性分析
(1)查看变量含义
笔者在本次项目使用的数据集是:“Credit Approval.csv”(来自UCI机器学习存储库)[1]首先,笔者对数据集进行探索性分析。通过data.head()命令查看原始数据集,如图1所示:
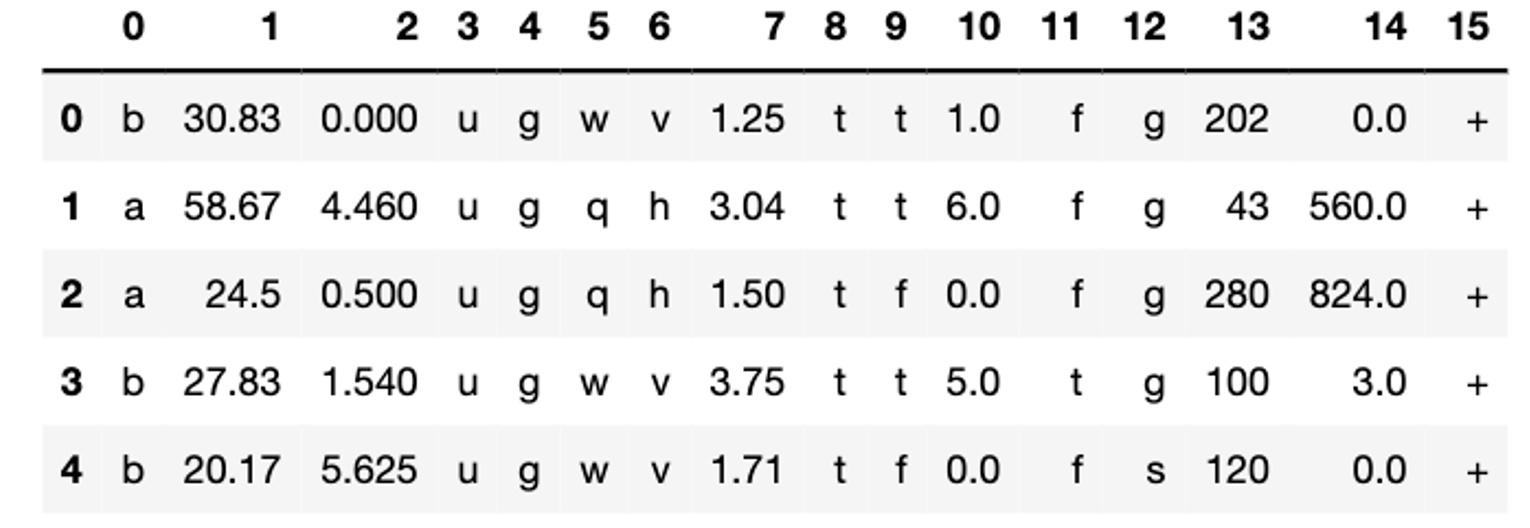
图1 data.head()命令查看原始数据集
可以看到,为了保护隐私,这个数据集的特征名称已经被匿名化了,所以数据集的看起来不知所云。通过查阅资料[2],笔者对数据集有了清晰的了解(表1):前15个变量是信用申请属性,Approved是信用审批状态,其值为“+”或“-”,表示是否已通过信用卡审批。
表1:数据集特征含义
| 列 | 属性 | 类型 | 数据 |
|---|---|---|---|
| 0 | Male(性别) | chr | b, a |
| 1 | Age(年龄) | chr | continuous. |
| 2 | Debt(债务) | num | continuous. |
| 3 | Married(婚姻) | chr | u, y, l, t. |
| 4 | BankCustomer(银行客户) | chr | g, p, gg. |
| 5 | EducationLevel(教育程度) | chr | c, d, cc, i, j, k, m, r, q, w, x, e, aa, ff. |
| 6 | Ethnicity(种族) | chr | v, h, bb, j, n, z, dd, ff, o. |
| 7 | YearsEmployed(工作年限) | num | continuous. |
| 8 | PriorDefault(违约记录) | num | t, f. |
| 9 | Employed(就业状况) | num | t, f. |
| 10 | CreditScore(信用评分) | num | continuous. |
| 11 | DriversLicense(驾照) | chr | t, f. |
| 12 | Citizen(公民) | chr | g, p, s. |
| 13 | ZipCode(邮政编码) | chr | continuous. |
| 14 | Income(收入) | num | continuous. |
| 15 | Approved(是否批准) | chr | +,- (class attribute) |
(2)处理Age变量(转换为num类型)
通过data.shape命令查看数据集格式,发现数据格式为(695, 16),通过data.info()查看数据集变量类型,如图2所示,数据集包含数值和非数值类型(float64和object)。其中,特征2、7、10和14是数值类型,其他都是非数值类型。
可以发现特征1为object 类型,但根据表3,这个变量代表的是Age,通过语句data[1] = pd.to_numeric(data[1])将其转换为num类型,以便后续的处理。这里需要注意的是这个变量因为存在缺失值为“?”,所以再转换类型前需要先通过data.replace(‘?’, np.NaN, inplace = True)语句将“?”替代为空值。(笔者刚开始没有先对Age变量进行处理,是后面使用LabelEncoder对数据集做数值变换才发现问题,所以才返回到开头这里先处理Age变量)
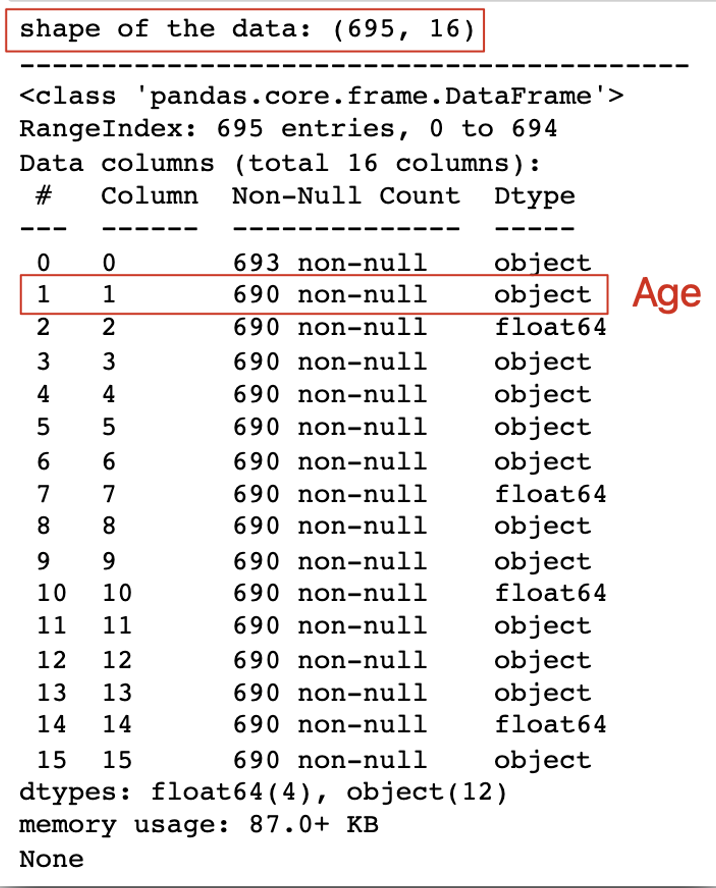
图2 data.shape和data.info() 查看数据集大小和类型
(3)对数值类型进行描述性统计
进一步地,笔者使用data.describe()语句查看连续型数值的描述性统计信息,如最小值、最大值、平均值和标准差,同时,可以看到该数据集特征范围不一致(0-28、0-67、0-100000)。如图3所示,列1、2、7、10、14分别代表Age(年龄)、Debt(债务)、YearsEmployed(工作年限)、CreditScore(信用评分)、Income(收入)。
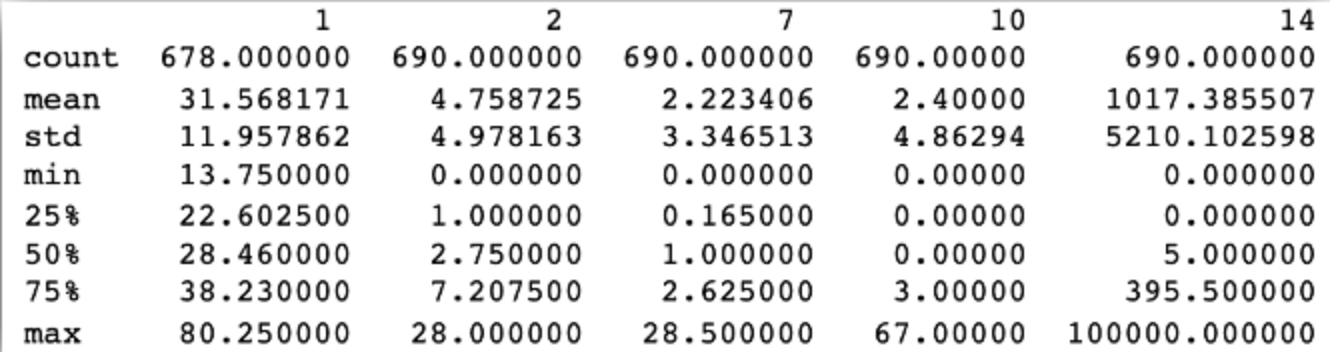
图3 data.describe()查看连续型数值的描述性统计信息
数据预处理
可以看到数据集混合了数值型和非数值型数据,此外还包含了许多缺失值,所以接下来必须对数据集进行预处理。这里提出的一个问题是:为什么不能直接忽略缺失值?因为忽略缺失值会严重影响机器学习模型的性能。在忽略缺失值的同时,机器学习模型可能会错过对其训练有用的数据集信息,同时也有许多模型不能自动处理缺失值(如 LDA)。
(1) 处理缺失值
首先,通过查看数据集,发现数据集中的缺失值被标为 “?”,笔者先通过data.replace(‘?’, np.nan)语句暂时用NaN替换这些缺失值的“?”
对于数值型缺失值的处理,有两种方法,一是简单地使用均值插补,用特征值的平均值来替代缺失值;二是检查数值之间的关系并使用线性回归来替代缺失值。这里笔者简单使用data.fillna(data.mean(), inplace=True)语句进行均值插补。(注意:这里只是处理了数值列中的缺失值,均值插补对非数值列中的缺失值不起作用)
对于非数值型缺失值的处理,笔者使用出现频次最高的值进行插补(关键语句:data= data.fillna(data[col].value_counts().index[0])),一般而言,在为分类数据插补缺失值时,这是一种常见且有效的做法[3]
最后,通过print(data.isnull().values.sum())语句计算数据集中的 NaN 数量并打印进行验证,可以看到这是数据集中缺失值数量为0(见jupyter文件)。
(2) 将非数值数据转换为数值型数据
接下来需要将所有非数值值转换为数值值。这是因为这不仅计算更快,而且许多机器学习模型都要求输入的数据为数值型格式。笔者在这里使用的工具是LabelEncoder[[4]](#_ftn4),完成将离散型的数据转换成0到n−1之间的数,n是一个列表的不同取值的个数,即某个特征的所有不同取值的个数。
from sklearn.preprocessing import LabelEncoder #导入标签编码器
le = LabelEncoder() # 实例化
for col in data: # 迭代每列的所有值并提取它们的数据类型
if data[col].dtype=='object': # 判断数据类型是否为对象类型
data[col]=le.fit_transform(data[col]) #使用LabelEncoder做数值变换
data.tail(15)
结果如图4所示,数据集已经全部都转化为数值型数据。
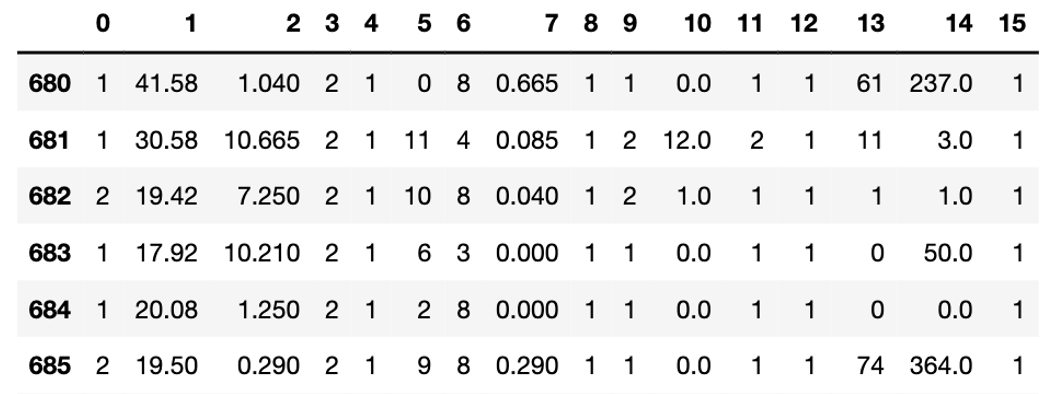
图4转化为数值型数据
(3) 将数据拆分为训练集和测试集
理想情况下,不应使用测试集中的任何信息来扩展训练集,接下来笔者将数据集分成训练集和测试集。此外,在此次预测信用卡审批中,像DriversLicense和ZipCode这样的特征并不是很重要,所以笔者进行了特征选择,在这里将这两个特征去除,以设计具有最佳特征集的机器学习模型。
from sklearn.model_selection import train_test_split
#去掉特征 11 和 13 并将 DataFrame 转换为 NumPy 数组
data = data.drop([11, 13], axis=1)
data = data.values
#将特征和标签分离到单独的变量中
X,y = data[:,0:13] , data[:,13]
# 分成训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.33, random_state=42)
最终的数据格式下表2所示:(注意,训练样本中X是大写的,而标签y是小写的,因为矩阵习惯用大写字母表示,向量习惯用小写字母来表示)
表2:数据集变量解释表
| 变量 | 含义 | 大小 |
|---|---|---|
| data | 整个数据集 | (695, 14) |
| X_train | 训练集样本 | (465, 13) |
| y_train | 训练集标签 | (465,1) |
| X_test | 测试集样本 | (230,13) |
| y_test | 测试集标签 | (230,) |
(4) 将数据标准化
如在PCA中使用的,笔者同样使用MinMaxScaler方法对数据进行标准化。
#实例化 MinMaxScaler 并使用它重新缩放 X_train 和 X_test
scaler = MinMaxScaler(feature_range=(0, 1))
rescaledX_train = scaler.fit_transform(X_train)
rescaledX_test = scaler.fit_transform(X_test)
使用KNN算法对数据集进行分类预测
(1)KNN算法描述
KNN算法原理较为简单,其算法描述如下图5所示,笔者不再进行论述。

图5 KNN算法描述
(2)具体实现
首先构建KNN类对象,步骤如下:
(1)计算测试数据与各个训练数据之间的距离;
(2)按照距离的递增关系进行排序;
(3)选取距离最小的K个点;
(4)确定前K个点所在类别的出现频率;
(5)返回前K个点中出现频率最高的类别作为测试数据的预测分类。
具体实现如下所示,笔者对每一行代码都进行了注释。值得注意的是,这里笔者原先直接使用了数组类型进行运算,结果出现了广播扩展问题,经过查阅资料,发现ndarray数组可以自己广播扩展然后对位运算,所以在开始就把X,y转化成ndarray数组类型,再进行运算。
class KNN1:
#初始化方法,k表示邻居的个数
def __init__(self, k):
#用当前的k来初始化KNN1对象中的k
self.k = k
# X: 训练集样本,类数组类型; y:训练集标签,类数组类型
def fit(self, X, y):
# 把X,y转化成ndarray数组类型
self.X = np.asarray(X)
self.y = np.asarray(y)
# 根据参数传递的样本,对测试集样本进行预测。X: 训练集样本,类数组类型;
def predict(self,X):
X = np.array(X)
# 储存预测的结果,数组类型
result = []
# 对ndarray数组进行遍历,每次取数组中的一行。
for x in X:
# 求测试集中的每个样本与训练集中所有点的距离。
# x代表测试集中的一行,X代表训练集中的所有行。ndarray数组可以自己广播扩展然后对位运算。
dis = np.sqrt(np.sum((x - self.X) ** 2,axis=1))
# argsort可以将数组排序后,每个元素在原数组中的索引位置。
index = dis.argsort()
# 进行截断,只取前k个元素【取距离最近的k个元素的索引】
index = index[:self.k]
# 返回数组中每个元素出现的次数。元素必须是非负的整数。
count = np.bincount(self.y[index])
# 返回ndarray数组中,值最大的元素对应的索引,该索引就是预测判定的类别。
result.append(count.argmax())
return np.asarray(result)
由于KNN算法对K的选取很敏感,笔者设置maxK变量控制K进行迭代运行(K只取奇数),并创建KNN对象,对数据集进行预测,得到每个K下的正确率,储存在rate_set列表。并计算最高准确率、最低准确率及其对应的K值、平均准确率和方差,并进行可视化。
rate_set = []
maxK = 101 #控制K的大小
for k in range(1,maxK): #迭代K
if k % 2 == 1:
knn = KNN1(k) # 创建KNN对象
knn.fit(X_train,y_train) # 进行训练
result = knn.predict(X_test) # 进行测试,获得测试的结果
accRate = np.sum(result == y_test)/len(result) # 计算正确率
rate_set.append(accRate) #添加到list
(3)项目结果分析
从表3可以看出,根据maxK的变动,可以看到KNN对此数据集分类预测的最大准确率为73.04%,此时k=3,可能由于样本量过少,这个准确率表现较为一般。且随着k的增加,当k达到255后,算法的准确率将稳定在64.63%,保持在最低准确率。
表3:k变动时,KNN算法准确率数据
| maxK | 最高准确率(k) | 最低准确率(k) | 平均准确率 | 方差 |
|---|---|---|---|---|
| 21 | 73.04% (k=3) | 70.43% (k=1) | 72.26% | 0.01% |
| 51 | 73.04% (k=3) | 69.13% (k=29) | 71.29% | 0.02% |
| 101 | 73.04% (k=3) | 68.70% (k=65) | 70.44% | 0.02% |
| 201 | 73.04% (k=3) | 62.17% (k=195) | 68.26% | 0.08% |
| 301 | 73.04% (k=3) | 54.78% (k=255) | 64.63% | 0.34% |
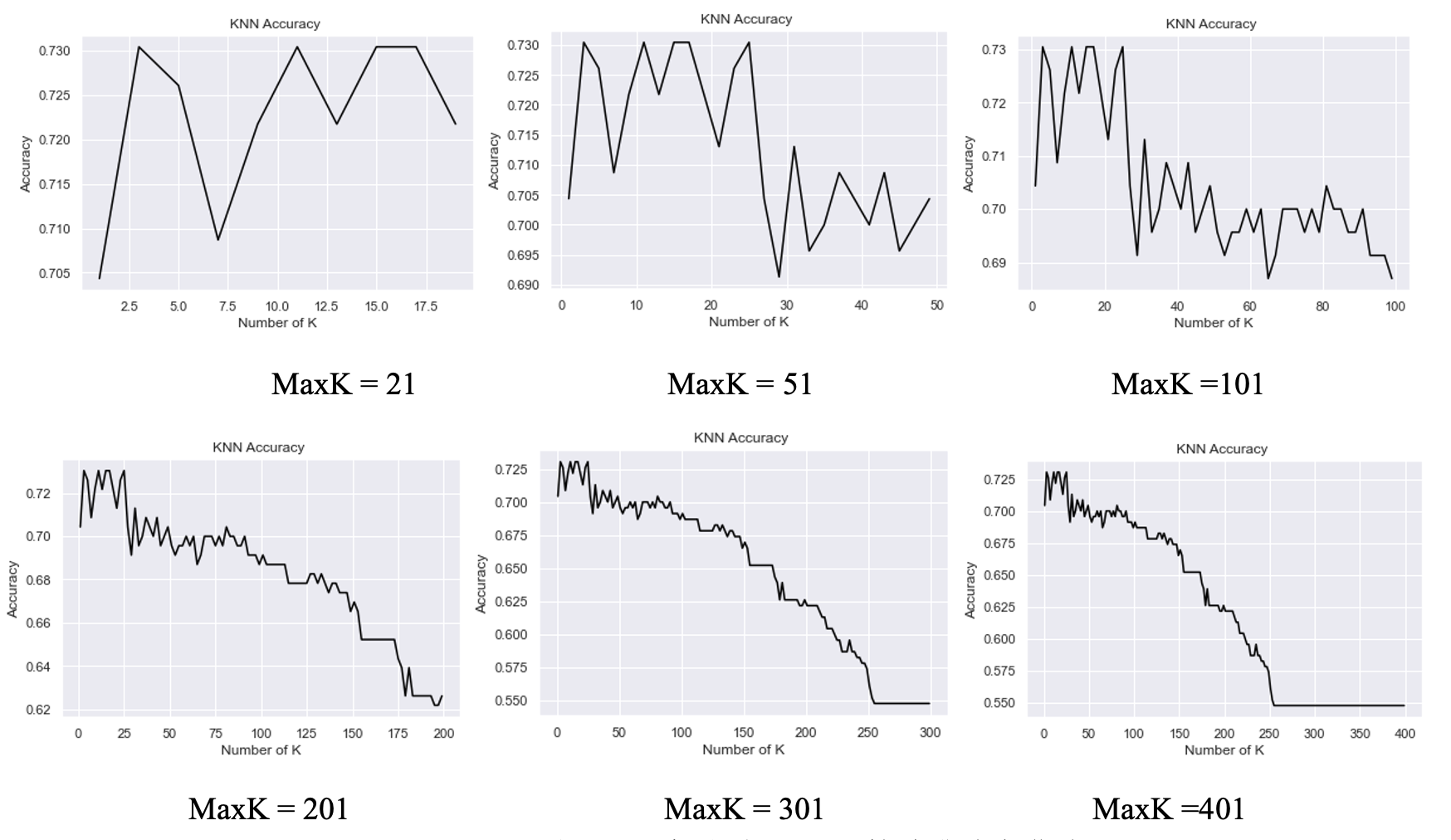
图6:k变动时,KNN算法准确率曲线
从样本数据考虑:PCA降维后再使用KNN算法
笔者考虑到可能是因为样本数据的原因,所以尝试将数据进行PCA降维后再使用KNN算法。
(1)封装PCA函数对象
首先对前面所详细叙述的PCA算法进行封装,实现通过输入要降维的数据和要求的方差解释率,实现对数据进行降维,结构如下所示:
1. class PCApercent(object):
2. def __init__(self, X, percentage):
3. def percent2n(self, eigVal): # 通过方差百分比选取前n个主成分
4. def _fit(self): #PCA算法
5. def fit(self):
6. def show(self): #画碎石图
(2)对样本数据X(不包含标签数据)进行PCA降维
从图22中可以看到99.9999%的方差解释率下,将13维度保留5个主成分,从碎石图可以看到,第1个主成分已经解释了99.9%的数据,笔者为了保留几乎完全的数据信息,将方差解释率提高到99.9999%。同样进行训练集、测试集拆分和数据归一化,可以看到X_train和X_test的大小变为(465,5)和(230,5)
#打印原始数据集
data = np.mat(pd.DataFrame(X))
print("Original dataset = {}*{}".format(data.shape[0], data.shape[1]))
#进行PCA降维
pca = PCApercent(data,0.999999) #方差解释率要求为99.9999%
pca.fit()
X = pca.low_dataMat #将得到降维后的数据还是存储到X
print(X.shape)
#方差解释率碎石图可视化
pca.show()
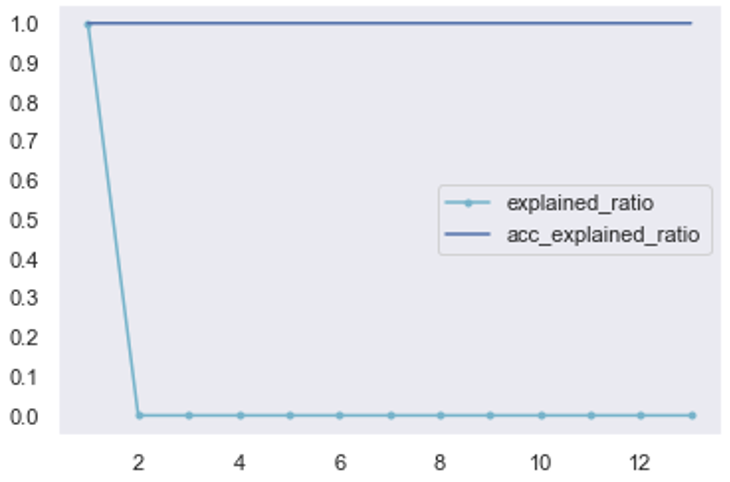
图7 对样本数据X进行PCA降维
(3)PCA_KNN分类
同样使用KNN分类器,通过k进行迭代和可视化,结果得到,当k=25时,分类的准确率达到最高,为74.35%,这个准确率比未降维前的最高准确率提高了1%,效果不是很明显。

图8:k变动时,PCA_KNN算法准确率曲线
(4)降维前后k的对比分析
对比当未降维前,k=3时取得最大准确率,降维后,k=25时取得最大准确率,这是因为k的选择反映了训练误差(近似误差)与测试误差(估计误差)的权衡,即:
若 k取较小值(模型复杂),预测实例较依赖于近邻样本,样本整体利用率低,模型对噪声数据敏感,且可能出现训练误差小(过拟合)、测试误差大的情况;
若 k值较大(模型简单),预测实例可利用较多的样本信息,模型抗干扰性强,但计算复杂,且可能出现训练误差大(欠拟合)、测试误差小的情况。
从算法设计考虑: KNN-kd tree算法
(1)kd树介绍
上述实现KNN算法时,笔者使用的是最简单的线性扫描的方式,即计算所有样本点与输入实例的距离,再取k个距离最小的点作为k近邻点。而KNN主要考虑的问题是如何在训练样本集中快速k近邻搜索,所以另一种更优化的想法是,构建数据索引,即通过构建树对输入空间进行划分,kd树就是此种实现。
kd树(k-dimension tree,k是指特征向量的维数),是一种存储k维空间中数据的平衡二叉树型结构,主要用于范围搜索和最近邻搜索。kd树实质是一种空间划分树,其每个节点对应一个k维的点,每个非叶节点相当于一个分割超平面,将其所在区域划分为两个子区域。kd树的结构可使得每次在局部空间中搜索目标数据,减少了不必要的数据搜索,从而加快了搜索速度。
(2)kd树具体实现
kd树的具体实现包括Step1 :构建kd树和Step 2:在kd树中搜索输入样本的k近邻,由于篇幅所限,笔者在这里只阐述实现思路,具体代码请见附件。
表4:knn – kd树具体实现思路

(3) KNN-kd tree 分类结果
同样通过k进行迭代和可视化,结果得到,当k=7时,分类的准确率达到最高,为87.39%,这个准确率比原始KNN的最高准确率提高了14.35%(87.39%-73.04%),效果提升明显。且当k=1时,算法的准确率最低,但也达到了80.87%。
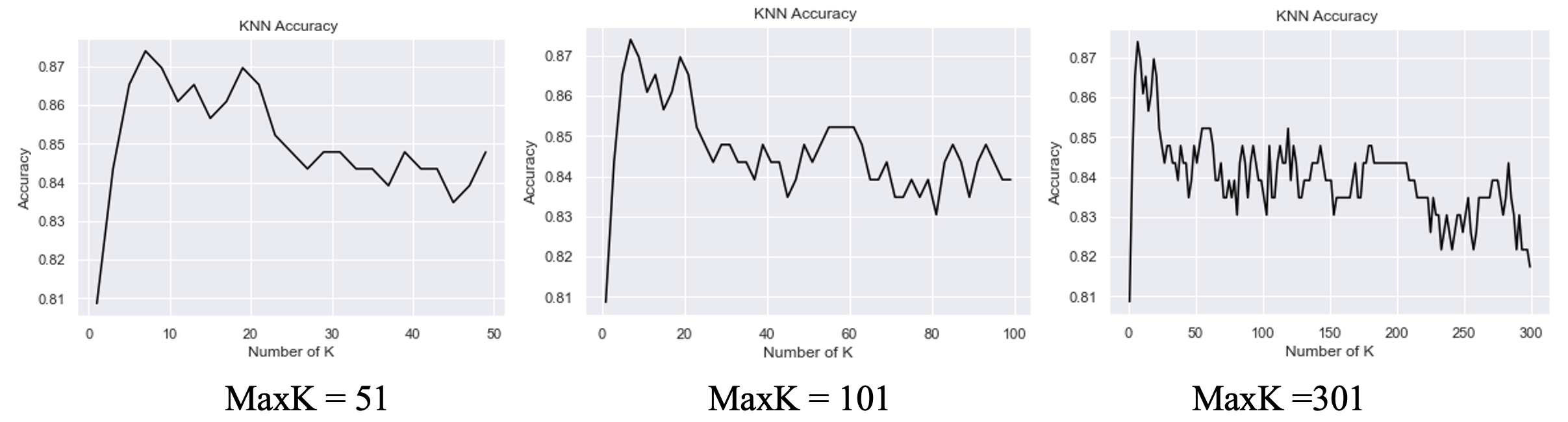
图9:k变动时,KNN_kd tree算法准确率曲线
体会
在这个过程中遇到最主要的困难是两个,一个是如何将算法进行封装调用,并且根据变量进行可视化,需要细心考虑整个数据集整体的变量;另一个是KNN kd tree算法笔者是自编实现的,这个过程有点复杂,虽然借鉴了很多网上的代码,但是还是要理解后根据自己的数据和可视化过程对函数进行封装。
总的来说,本次项目过程中也踩了很多坑,收获了很多经验。虽然为了整体项目的逻辑性,笔者耗费了很多时间,但是其实对于一个数据集如何去进行处理的问题,其实还有很多算法是笔者想继续进行尝试的。同时,整个过程也感受到了理解算法的推导过程多么地重要,这是单纯做一个调包侠所不能比拟的。笔者将继续探索和努力,将所学转换为所用。
源代码
关于本次项目的源文件可以在笔者的Github下载
├── KNN code.ipynb
└── T3.Credit Approval.csv
[1] UCI Machine Learning Repository: http://archive.ics.uci.edu/ml/datasets/credit+approval
[2] 参考:http://rstudio-pubs-static.s3.amazonaws.com/73039_9946de135c0a49daa7a0a9eda4a67a72.html
[3] 参考:https://www.datacamp.com/community/tutorials/categorical-data
[4] 参考:https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.LabelEncoder.html
[5] 参考:https://cloud.tencent.com/developer/article/1178474
[6] 参考:https://www.cnblogs.com/21207-ihome/p/6084670.html
[7] 参考:https://blog.csdn.net/sinat_34072381/article/details/84104440